1) Экскурс в теорию: угол между плоскостями (ВАС) и (САН)- двугранный угол (НАСВ) измеряется градусной мерой линейного угла L HCB , образованного лучами СВ и СН , имеющими начало на ребре (АС) и перепендикулярными к нему,
т.е. L HCB = 60⁰. (см. рис.).
2) Углом между прямой и плоскостью наз-ся угол между этой прямой и её проекцией на данную плоскость, тогда углом между катетом ВС и плоскостью (САН) является L L HCB = 60⁰ .
3) Угол между гипотенузой АВ найдём, рассмотрев ΔАВН - прям.:
sin L BAH = BH/AB = 0,5√3a/(a√2) =√6/4,
таким образом L BAH = arcsin √6/4.
ОТвет: 60⁰; arcsin √6/4.
УДАЧИ
AK=5√6 см, KB=10 см
Объяснение:
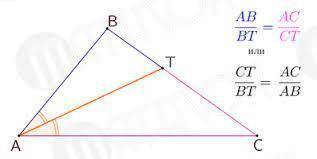
Теорема биссектрисы прикреплена в рисунке. По ней мы имеем:
BK/KC=AB/AC=20/10=2
BK=2KC; CB=BK+KC=15⇒2KC+KC=15
3KC=15; KC=15/3=5 см
BK=BC-KC=15-5=10 см
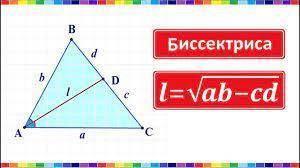
Вторая теорема биссектрисы также прикреплена к ответу. По ней имеем:
AK=√AB*AC-BK*KC=√200-50=√150=√25*√6=5√6
Далее идут доказательства верности ответа другими, тяжёлыми для понимания теоремами. Их не желательно употреблять, они здесь только ради утверждения компетентности моего 2-го ответа. (Ну и для того, чтобы похвастаться знаниями тоже)
Проверим ответ по теореме Стюарта:
AK²*BC=AB²*KC + AC²*BK - BC*KC*BK
AK²*15=400*5 + 100*10 - 15*10*5=2250
AK²=2250/15=150
AK=√150=√25*√6=5√6
ЧТД
Третья формула для нахождения биссектрисы
AK²=AB² * KC/BC + AC² * BK/BC - BK*KC
AK²=2000/15+1000/15-50=200-50=150
AK=√150=√25*√6=5√6
ЧТД
Правда я не знаю как тебе это объяснить