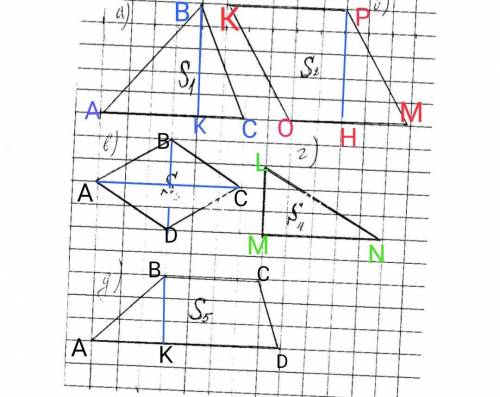
Объяснение:
1кл=1см
1) треугольник ∆АВС
Площадь треугольника равна половине произведения основания на высоту опущенную на это основание.
ВК- высота
S1=АС*ВК/2=6*5/2=15см² площадь треугольника ∆АВС
ответ: площадь треугольника ∆АВС равна 15см²
2) параллелограм КРМО.
РН-высота
S2=PH*OM=5*5=25 см² площадь параллелограма.
ответ: 25см²
3) ромб АВСD
AС и ВD диагонали ромба
Площадь ромба равна половине произведения двух диагоналей
S3=АС*BD/2=4*6/2=24/2=12см² площадь ромба.
ответ: 12см²
4) ∆LMN
∆LMN- прямоугольный.
Площадь прямоугольного треугольника равна половине произведения двух катетов.
S4=LM*MN/2=3*5/2=7,5см² площадь треугольника ∆LMN
ответ: 7,5см²
5) трапеция ABCD.
Площадь трапеции равна произведению средней линии трапеции на высоту.
ВК- высота трапеции.
S4=BK*(BC+AD)/2
S4=3*(4+8)/2=3*12/2=36/2=18см² площадь трапеции
ответ:18см²
Давай, равнобокая трапеция это равнобедренная трапеция, боковые стороны равны
1)Обозначим ее АВСД АД -нижнее основание ВС- верхнее
опустим высоту из вершины В на нижнее основание , получаем прямоугольный треугольник АНВ у которого угол А = 60 ( по условию) , значит другой угол этого треугольника = 30 градусов ( сумма острых углов в прямоугольном треугольнике = 90 градусов)
2)По условию боковая сторона = 4 = АВ , есть правило что катет лежащий против угла в 30 градусов равен половине гипотенузы,следовательно, АН= 1/2 АВ то есть = 2
3)Опустим высоту из вершины С , назовем СР, треугольники АНВ= СРД ( по 1 признаку) , значит стороны АН=РД=2
4) Вся сторона АД= 12, а ВС= НР значит отнимаем от АД-АН-РД= 8
ответ :8
1) По т.Пифагора СА=√(АВ²+ВС²)=√(7²+(7√3)²)=√(49+147)=√196=14 (см).
2) sin∠C=AB/AC=7/14=1/2, ∠C=30°.
ответ: 14 см; sin∠C=1/2, ∠C=30°.
№2. 1) ΔAHB - прямоугольный, tg∠B=BH/AH, ⇒AH=BH/tg∠B=4/tg50°;
2) ΔCHB - прямоугольный, tg∠C=BH/HC, ⇒HC=BH/tg∠C=4/tg70°;
3) AC=AH+HC=4/tg50°+4/tg70°.
Для приблизительного вычисления стороны АС можно воспользоваться таблицами Брадиса для тангенса: tg50°≈1,1918; tg70°≈2,747.
AC=4/1,1918+4/2,747≈3,4+1,5=4,9 (см).
ответ: 4/tg50°+4/tg70°≈4,9 (см).