ABC - равнобедренный треугольник, AC = 8, P_ABC = 18, V_тела вращения = V_цилиндра с высотой равной основанию треугольника и радиусом равным высоте треугольника - 2*V_конуса с радиусом основания равным высоте треугольника и высотой равным половине основания треугольника
V_цилиндра = pi*r^2*h
Радиус найдём воспользовавшись теоремой Пифагора и тем, что наш треугольник равнобедренный. AB = BC = (P_ABC - AC)/2 = (18-8)/2 = 5, r_основания цилиндра (=высоте треугольника) = V(AB^2+(AC/2)^2) = V25 + 16 = V41 (Корень), (высоту искали из прямоугольного треугольника ABC', C' делит AC пополам)
V_цилиндра = pi*r^2*h= pi * 41 * 8 =328pi
V_конуса = 1/3*pi*(r_конуса)^2*h_конуса = 1/3*pi*41*4 =123/3*pi
V_тела вращения = V_цилиндра - 2*V_конуса = 328pi - 246/3*pi = (328-82)pi = 246pi
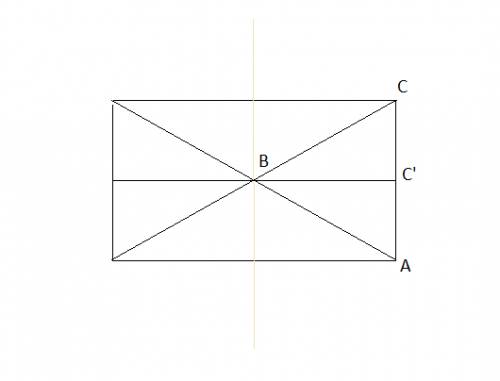
Проведем высоту ВН
Высота равнобедренного треугольника, проведенная из вершины на его основание, является биссектрисой и медианой ⇒
АН = НС = АС/2 = 16/2 = 8 см.
Рассмотрим прямоугольный ΔВНС: По теореме Пифагора
ВС² = ВН² + НС²
ВН² = ВС² - НС² = 10² - 8² = 100 - 64 = 36
⇒ ВН = 6 см.
Площадь треугольника рассчитывается по формуле:
где р - полупериметр
ответ: см.
см.