Формула радиуса окружности, описанной около правильного треугольника 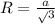 ⇒
⇒
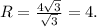
Объяснение:
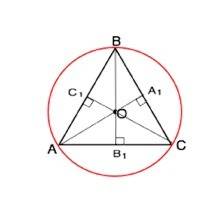
Центром описанной около треугольника окружности является точка пересечения его срединных перпендикуляров.
В проаильном треугольнике срединные перпендикуляры - высоты, биссектрисы, медианы.
Все стороны правльного треугольника равны, и все углы равны 60°.
Так как срединные перпендикуляры еще и медианы, точка пересечения делит их в отношении 2:1, считая от вершины. Все медианы правильного треугольника равны, а больший отрезок медианы - радиус описанной окружности.
ВВ1=АВ•sin60°
BB1=4√3•√3/2=6
R=BO=6:3•2=4 (ед. длины)
другая сторона 8*2=16см
34*34=15x*15x+8x*8x
1156=225x*x+64x*x
1156=289x*x
x*x=1156/289
x*х=квадратный корень4
Х=2