Высота, проведённая из вершины прямого угла прямоугольного треульника, равна 6 см и делит гипотенузу на отрезки, один из которых больше другого на 5 см. найти стороны треугольника.
В прямоугольном треугольнике высота h, проведенная из вершины прямого угла к гипотенузе, равна Корню квадратному из произведения частей, на которые высота делит гипотенузу. Пусть Она часть - x? тогда вторая - х+5.
Решим уравнение и Найдем х.
Получим, что х=4 см, тогда вторая часть - 9 см. Вся гипотенуза - 13 см.
Остальные стороны находим по теореме Пифагора для каждого отдельного треугольника( т.к. высота h делит большой трейгольник на два маленьких прямоугольных треугольника).
1) Все диаметры окружности равны между собой – верно. Диаметр - отрезок, проходящий через центр окружности и равен двум радиусам. Все радиусы одной окружности равны.
2) Сумма углов любого треугольника равна 360 градусам – неверно. Сумма углов любого треугольника 180°
3) Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом. Верно. В параллелограмме противоположные стороны равны и параллельны. Если равны и соседние стороны, то все стороны равны. Параллелограмм, все стороны которого равны – ромб.
Если гипотенуза АВ параллельна оси Ох, то точки А и В - противоположные. A(-x1; y1); B(x1; y1); |AB| = 2x1 Точка С лежит между ними. C(x2; y2); -x1 < x2 < x1 |AC|^2 = (x2+x1)^2 + (y1-y2)^2 |BC|^2 = (x2-x1)^2 + (y1-y2)^2 По теореме Пифагора |AC|^2 + |BC|^2 = |AB|^2 (x2+x1)^2 + (y1-y2)^2 + (x2-x1)^2 + (y1-y2)^2 = 4x1^2 x2^2 + 2x1*x2 + x1^2 + 2(y1-y2)^2 + x2^2 - 2x1*x2 + x1^2 - 4x1^2 = 0 2x2^2 + 2(y1-y2)^2 - 2x1^2 = 0 x2^2 + (y1-y2)^2 - x1^2 = 0 (y1 - y2)^2 = x1^2 - x2^2 Вспомним, что это парабола y = x^2, и y1 = x1^2; y2 = x2^2 (x1^2 - x2^2)^2 = x1^2 - x2^2 Число равно своему квадрату, значит, оно равно 0 или 1. (x1^2 - x2^2) = (y1 - y2) = 0 или 1 Но 0 разность ординат точек А и С равняться не может, значит, y1 - y2 = 1 Но разность ординат - это и есть высота треугольника.
В прямоугольном треугольнике высота h, проведенная из вершины прямого угла к гипотенузе, равна Корню квадратному из произведения частей, на которые высота делит гипотенузу. Пусть Она часть - x? тогда вторая - х+5.
Решим уравнение и Найдем х.
Получим, что х=4 см, тогда вторая часть - 9 см. Вся гипотенуза - 13 см.
Остальные стороны находим по теореме Пифагора для каждого отдельного треугольника( т.к. высота h делит большой трейгольник на два маленьких прямоугольных треугольника).
Получим, один катет равен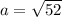
, а второй - 
.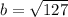