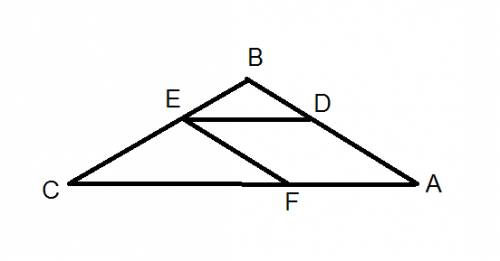
Второй случай решения состоит в том, что общий угол у ромба и у треугольника находится при основании треугольника.
Имеется рисунок (вложение)
известно, что AC=12, BC=9, AB = 9.
Из свойства равнобедренного треугольника следует, что угол BAC равен углу ACB. (1)
Из параллельности сторон в параллелограмме (а ромб является частным случаем параллелограмма) следует, что угол BDE равен углу DAF, а угол DAF равен углу EFC (2).
AE - биссектриса угла ВАС (из свойств ромба). По теореме о биссектрисах
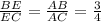 ,
,
откуда 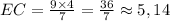
Так как этот треугольник - равнобедренный (из 1 и 2), то 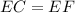 , где EF - сторона ромба.
, где EF - сторона ромба.
Пусть AH=x, тогда по свойству катета, лежащего против угла в 30° AB=2x.
По теореме Пифагора
x=-1 не удовлетворяет условиям задачи.
AB=CD=2*1=2
∠A=60° ⇒ ∠D=180-60=120°
По теореме косинусов
ответ: 2√7