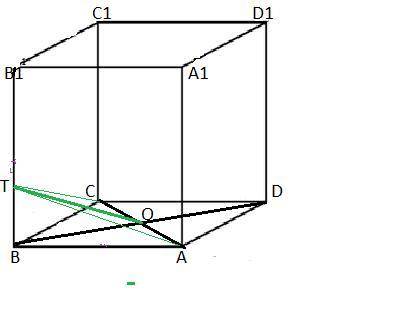
В кубе ABCDA1B1C1D1, ребра которого равны 4, на ребре BB1 взята точка T так, что BT:TB1=1:3. Найти синус угла между плоскостями (АВС) и (АТС)
Объяснение:
Т.к. BT:TB₁=1:3 и ВВ₁=4 ,то ВТ=4:4*1=1 (см).
Из ΔАВС-прямоугольного , по т. Пифагора найдем
АС=√(4²+4²)=4√2 (см). Значит ВD=4√2 см⇒ВО=2√2 см.
В кубе все грани квадраты⇒АС⊥ВD и ТВ⊥ВD ⇒ по т. о трех перпендикулярах ∠ТОВ-линейный угол между плоскостями (АВС) и (АТС).
ΔВТО-прямоугольный , по т. Пифагора ТО²=ВТ²+ТО². ТО=3 см.
sin∠ТВО=ТВ/ТО, sin∠ТВО=1*3.
Синус угла между плоскостями (АВС) и (АТС) равен 1/3.
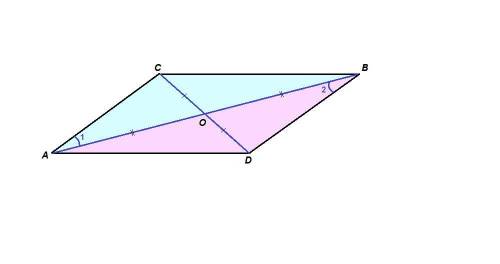
ответ: ∠АСВ = 112°
Объяснение:
1. АО = ОВ и CO = OD по условию,
∠АОС = ∠BOD как вертикальные, значит
ΔАОС = ΔBOD по двум сторонам и углу между ними.
Из равенства треугольников следует, что
АС = BD и ∠САО = ∠DBO.
2. Тогда в треугольниках АСВ и BDA:
АС = BD, ∠1 = ∠2, AB - общая сторона, значит
ΔАСВ = ΔBDA по двум сторонам и углу между ними.
3. ∠1 = ∠2, а эти углы - накрест лежащие при пересечении прямых АС и BD секущей АВ, значит
АС║BD.
∠АСВ + ∠CBD = 180°, так как эти углы соответственные при пересечении параллельных прямых АС и BD секущей ВС, тогда
∠АСВ = 180° - ∠CBD = 180° - 68° = 112°
x^2 = 225-81 = 144 => x = 12 см. В итоге видим, что высота второго треугольника больше первого в 2 раза. Тогда ребра и основание равны соответственно 30 и 36 см. Периметр равен 96 см.