Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а) 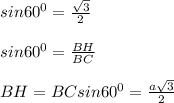
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
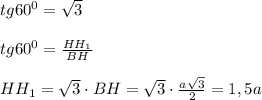
в) Найти площадь боковой поверхности - самая простая часть этого задания:
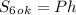 , где
, где 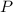 и
и  - периметр основания и высота пераллелепипеда соответственно.
- периметр основания и высота пераллелепипеда соответственно.

г) 
Объяснение:
1) Так как искомый центр гомотетии лежит на одной прямой с точками Х и X', то для нахождения центра проведем прямую XX'.
Условия заданий приводятся в учебных целях и в необходимом объеме — как иллюстративный материал. Имя автора и название цитируемого издания указаны на титульном листе данной книги. (Ст. 19 п. 2 Закона РФ об авторском праве и смежных правах от 9 июня 1993 г.)
2) Так как N = 2, то по определению гомотетии ОХ' = 20Х, где О — центр гомотетии, значит, отложим от точки X' отрезок ОХ' = 2ОХ и получим искомую точку О.
A*n=180*n-360;
A*n-180*n=-360;
n(A-180)=-360;
n=-360/(120-180);
n=360/60;
n=6. ответ многоугольник имеет 6 сторон