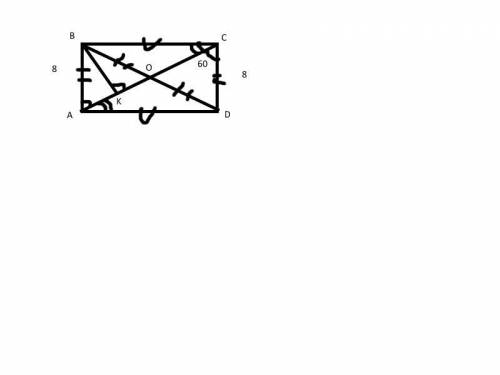
Дано: ABCD - прямоугольник
BK⊥AC
∠ACD=60°
AB=8 см
Найти: BD = ?
OK = ?
Т.к ABCD - прямоугольник, то AB=CD=8 см
∠OCD=∠BAO (н/л BC || AD и сек. AC) = 60°
∠BCO=∠OAD (н/л) = 90-60=30°
В прямоугольном ΔABC, ∠B=90°, ∠ACB=30°. Напротив угла в 30° в прямоугольном Δ лежит катет, равный половине гипотенузы => AB=0,5*AC => 8=0,5*AC => AC=8:0,5 => AC=16
Диагонали в прямоугольнике точкой пересечения делятся пополам => AO=OC=8 см.
ΔOCD - р/б т.к OC=CD => ∠COD=∠ODC. Сумма углов в треугольнике равна 180° => ∠COD=∠ODC= (180°-60°)/2=60° => ΔOCD - равносторонний по признаку => OD=OC=CD=8 см
BO=OD (диагональ делится пополам точкой пересечения)
BD=2*OD
BD=2*8
BD=16 см
ΔBOA - равносторонний (AB=BO=AO=8 см) => BK - высота, биссектриса и медиана => OK= 0,5*AO; OK=0,5*8; OK=4
ответ: BD = 16 см; OK = 4 см
Объяснение:
1.
Не думаю, что в 9 классе проходят ряда Тейлора, наверняка хоть что-то из тригонометрических функций надо было найти по таблице, потому что чаще всего эти функции находят именно по определённым таблицам.
Наверняка ты должен был найти синус по таблице, но почему бы и не найти его другим ?
Так что, вычислим синус с кода(язык — Java), всё очень просто, эта функция из самых лёгких:
//////////////////////////////////////////////////////////////////
public class MyClass {
public static void main(String args[]) {
//угол должен быть в радианах
double radian = 2.6180;
System.out.println(Math.sin(radian));
}
}
///////////////////////////////////////////////////////
Output: 0.5.
Синус равен: 0.5.
А вот зная синус, мы можем простой формулой найти и косинус: 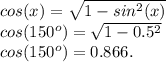
Тангенс найдём по такой формуле:
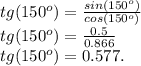
Вывод: sin = 0.5; cos = 0.866; tg = 0.577.
2.
Зная 2 стороны треугольника, и угол между ними, можем найти третью сторону по теореме косинусов:
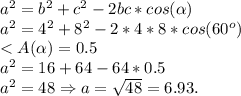
Площадь найдём по теореме Герона: 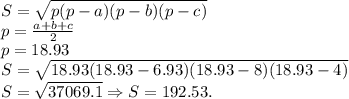
3.
Оставшийся угол равен: 180-(135+30) = 15°
Теперь, зная одну сторону, и углы прилежащие к нему углы, найдём остальные стороны теоремой синусов:
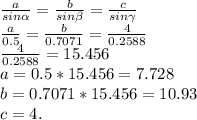
Вывод: b = 10.93.
5.
Для вычисления радиуса вписанной окружности в треугольнике — сначала найдём площадь этого треугольника — по теореме Герона: 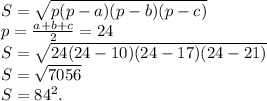
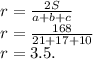
Вывод: r = 3.5.
6.
Зная все стороны, можем найти медианы, медиана, проведённая к стороне 12-и см (b) — равна:
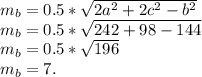
Вывод: медиана, проведённая к самой большой стороне — равна 7 см.
b=3/5корень11
а=AC^2-b^2 тут подставь и все
Это прямоугольный треугольник значит площадь его такова: S=ab/2 тогда s=3/5корень 11×99/5×1/2