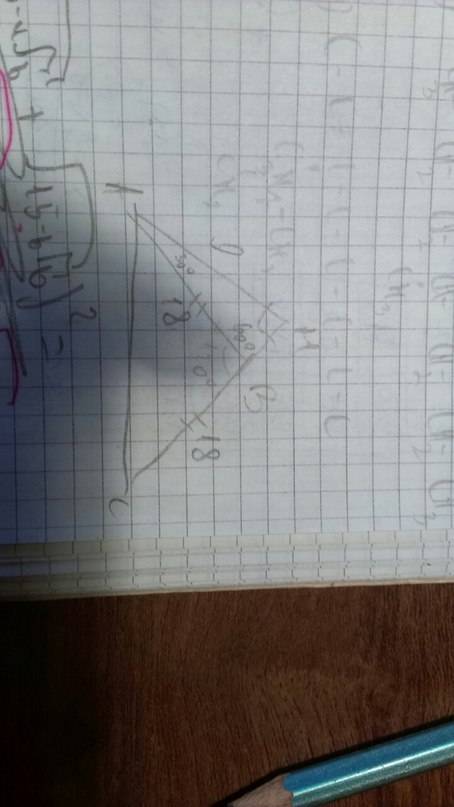
∠CDE составляет одну часть, ∠ADE - 8 таких частей, всего 9 частей.
∠CDE = 90° : 9 = 10°
Сумма острых углов прямоугольного треугольника 90°, тогда из ΔCDE:
∠DCE = 90° - ∠CDE = 90° - 10° = 80°
Диагонали прямоугольника равны и точкой пересечения делятся пополам, тогда ΔCOD равнобедренный (CO = OD), значит углы при его основании равны:
∠OCD = ∠ODC = 80°.
В ΔOCD находим третий угол:
∠COD = 180° - (∠OCD + ∠ODC) = 180° - 160° = 20° - угол между диагоналями.
Объяснение:
Подпишись на меня в ютубе мой канал. LIXORADKA 43. Буду тебя там ждать)
Вписанная окружность - когда в треугольник вписать окружность, притом только одну. (тобишь окружность внутри треугольника и три его стороны идут как касательные к окружности), и в этом же случае треугольник описан вокруг окружности
здесь игра слов - что Вписано то внутри , что Описано то снаружи
чтобы построить вписанную окружность (тоесть описанный треугольник) берём произвольно окружность , и рисуем на ней хорду например АВ, с любой стороны от хорды на окружности отмечаем точку С и чертим отрезки АС и ВС
чтобы построить описанную окружность (тоесть вписанный треугольник)
рисуем любой треугольник АВС, с двух углов треугольника опускаем перпендикуляры , точку их пересечения обозначаем за О (это центр окружности) , расстояние от О до точки А,В или С это радиусы окружности, задаём радиус циркулю, ставим циркуль в О и рисуем окружность