Рассмотрим ΔABC - равнобедренный; AB=BC=25 см;
BD - медиана ⇒ AD=DC=14:2=7 см
Т.к. ΔABC - равнобедренный, то BD - является и высотой, и биссектрисой еще.
Рассмотрим ΔABD - прямоугольной; ∠D - прямой, AB=25см; AD=7 см
по т. Пифагора найдем BD
BD² = AB² - AD²
BD² = 25² - 7²
BD = 24 cм
Рассмотрим еще раз ΔABC:
по свойству медианы OD=1/3 * BD = 1/3 * 24 = 24 : 3 = 8 см
Рассмотрим ΔCOD - прямоугольный; ∠D - прямой; DC=7 см; OD=8 см
по т.Пифагора найдем OC
OC² = OD² + DC²
OC² = 8² + 7²
OC = 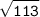 см
см
по свойству медианы 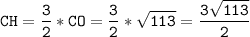 см
см
по свойству равнобедренного треугольника CH=AK= 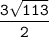 см
см
ответ: 24 см; 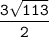 см;
см; 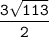 см
см
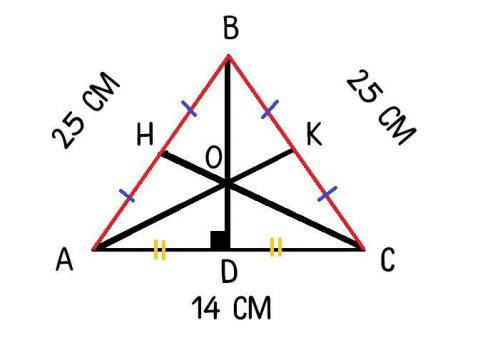
Рассмотрим ΔABC - равнобедренный; AB=BC=25 см;
BD - медиана ⇒ AD=DC=14:2=7 см
Т.к. ΔABC - равнобедренный, то BD - является и высотой, и биссектрисой еще.
Рассмотрим ΔABD - прямоугольной; ∠D - прямой, AB=25см; AD=7 см
по т. Пифагора найдем BD
BD² = AB² - AD²
BD² = 25² - 7²
BD = 24 cм
Рассмотрим еще раз ΔABC:
по свойству медианы OD=1/3 * BD = 1/3 * 24 = 24 : 3 = 8 см
Рассмотрим ΔCOD - прямоугольный; ∠D - прямой; DC=7 см; OD=8 см
по т.Пифагора найдем OC
OC² = OD² + DC²
OC² = 8² + 7²
OC = 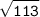 см
см
по свойству медианы 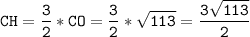 см
см
по свойству равнобедренного треугольника CH=AK= 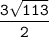 см
см
ответ: 24 см; 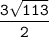 см;
см; 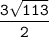 см
см

BA=(4 - 1; 5 - 2; -1 - 3)=(3;3;-4);
BC(0-1;-3-2;1-3)=(-1;-5;-2)
cosα=(-3 - 15 + 8)/√(9+9+16)*√(1+25+4)√=-10/√34*√30=--5/(4√2)