
Объяснение:
Дано:
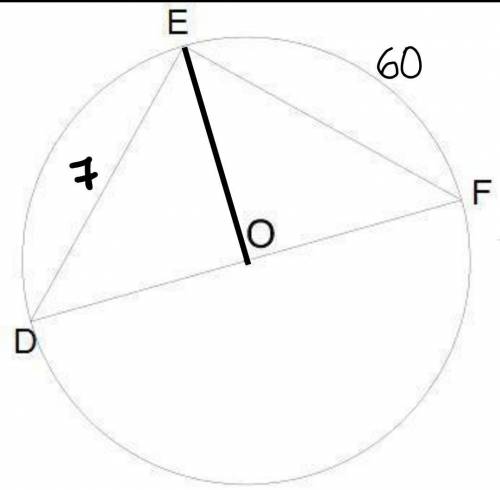
Окружность с центром в точке О;
Дуга ED=60°;
ED=7 см.
Найти: длину окружности.
Проведем ЕО.
Угол ЕОF – центральный и опирается на дугу EF, тогда угол EOF=дуга EF=60°.
Угол DOE=180°–угол EOF=180°–60°=120° (смежные углы)
DO=EO так как радиусы равны, следовательно ∆ЕОD – равнобедренный с основанием ED.
Углы при основании равнобедренного треугольника равны, тогда угол DEO=угол ODE=(180°–угол DOE)÷2=(180°–120°)÷2=60°÷2=30°.
По теореме синусов в ∆EOD:
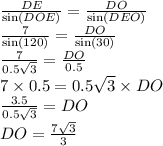
DO – радиус окружности.
C=2πr, где С – длина окружности; r – радиус окружности.
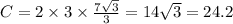
ответ: 24,2 см.
Касательные, проведённые к окружности из одной точки, равны. АВ=АС.
Прямоугольные треугольники АОС и АОВ равны т.к. ОС=ОВ и АО - общая сторона, значит ∠САО=∠ВАО=30° ⇒ ∠ВАС=60°.
В треугольнике АВС АВ=АС, ∠ВАС=60°, значит ∠АВС=∠АСВ=(180-60)/2=60°, значит ΔАВС правильный (равносторонний).
Доказано.