В треугольнике ABC, периметр которого равен 20 см ,вписан круг. Отрезок касательной проведенной к окружности параллельно стороне AC, размещенной между сторонами треугольника, равен 2,4 см. Найдите сторону AC.
Объяснение:
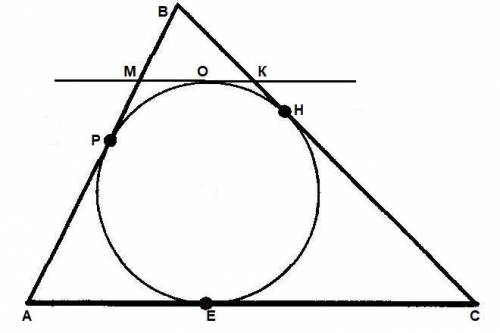
Пусть отрезок касательной проведенной к окружности параллельно стороне AC будет МК , МК=2,4 см.
Пусть точки касания располагаются так :
А-Р-В ,А-Е-С , В-Н-С , М-О-К.
ΔВМК подобен ΔВАС по двум углам : ∠ВМК=∠ВАС как соответственные и ∠В- общий.
Поэтому Р(МВК):Р(АВС)=к=МК:АС.
Выразим 1)Р(МВК), 2)АС используя свойство отрезков касательных.
1)Р(МВК)=2,4+МВ+ВК=
=2,4+(ВР-МР)+(ВН-КН)=
=2,4+(ВР-МО)+(ВН-КО)=
=2,4+(ВР+ВН)-(МО+КО)=
=2,4 +2ВР-2,4=2ВР.
Значит Р(МВК) =2ВР.
2)Р(АВС)=АВ+ВС+АС=
=(ВР+РА)+(ВН+НС)+АС=
=(ВР+АЕ)+(ВН+ЕС)+АС=
=(ВР+ВН)+(АЕ+ЕС)+АС=
=2ВР+2АС,
20=2ВР+2АС, 10=ВР+АС, ВР=10-АС.
Т.о Р(МВК):Р(АВС)=МК:АС ,
2ВР:20=2,4:АС,
АС*ВР=24 ( но ВР=10-АС), пусть АС=в ,
в(10-в)=24,
в²-10в+24=0, D=4 , в₁=4, в₂=6
АС=4см, Ас=6 см
a/sinα=2R - из теоремы синусов.
2R=3√3/sin60° (так как треугольник правильные все углы по 60°)
2R=3√3 / √3/2
2R= 3√3 * 2/√3
R=6/2 = 3
l=2π*3 ; l=6π (π=3,14)
l=18,84