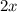 )
)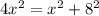
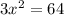
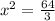
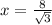
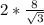 =
=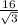
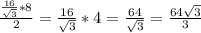 см²
см²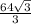 см²
см²
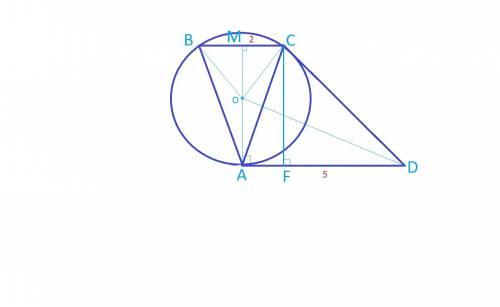
 трапеция
трапеция - описана около Δ
- описана около Δ 
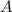 и
и 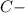 точки касания
точки касания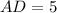
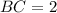
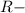 ?
?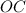 ⊥
⊥ 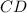
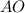 ⊥
⊥ 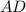
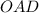 и Δ
и Δ 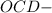 прямоугольные
прямоугольные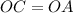 ( как радиусы)
( как радиусы)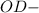 общая
общая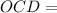 Δ
Δ 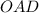 (по гипотенузе и острому углу)
(по гипотенузе и острому углу)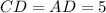
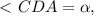 тогда
тогда 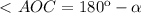
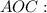
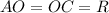

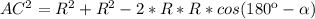
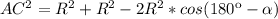
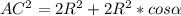


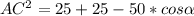
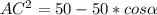
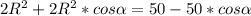
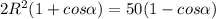
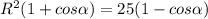
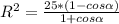
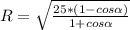 (1)
(1)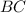 ║
║ 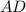
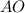 ⊥
⊥ 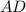
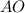 ∩
∩ 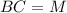 ⇒
⇒ 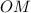 ⊥
⊥ 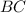
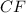 ⊥
⊥ 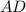
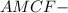 прямоугольник
прямоугольник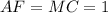
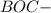 равнобедренный, значит
равнобедренный, значит 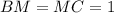
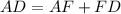
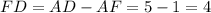
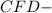 прямоугольный
прямоугольный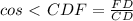
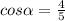
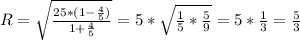
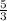
Нарисуем треугольник АВС, проведем высоту СН.
Обратим внимание на то, что в треугольнике АВС, так как СН перпендикулярно АВ,
косинус А можно выразить не только, как АС:АВ, но и АН:АС
Тогда из соs A=√51):10 получим отношение
АН:АС=√51):10
Произведение крайних членов пропорции равно произведению ее средних членов:
10 АН=12√51
АН=12√51):10
По т.Пифагора из треугольника АСН
СН²=АС²-АН²
СН²=144 -144·51:100
Приведем к общему знаменателю:
СН²=(144·100 -144·51):100
СН²=144(100-51):100
СН²=144·49:100
СН=12·7:10=84:10=8,4