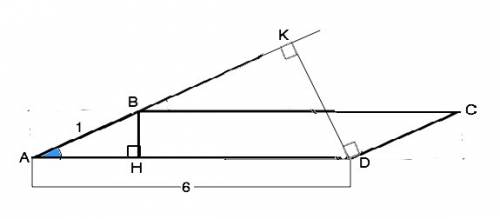
Одна из формул площади параллелограмма Ѕ=a•h. Очевидно, что при одинаковой площади большей будет высота, проведенная к меньшей стороне, и наоборот. Следовательно, искомой будет высота к стороне АВ ( или равной ей CD).
На рисунке в приложении высота к меньшей стороне АВ пересекается с ее продолжением. Из прямоугольного треугольника AKD высота DK=AD•sinA=6•1/3=2 (ед. длины)
Как вариант можно найти большую высоту иначе. Сначала найти длину меньшей высоты ВН=АВ•sinA, затем найти площадь S=ВН•AD и высоту DK=S:AB.
ответ:
ас = св = ва = а ( по условию) ==> ∆авс - равносторонний
проведем через пункт с прямую, параллельную прямой el, пункт пересечения этой прямой с прямой ав обозначим м
см ll el
по т. фалеса имеем
me/eb = cl/lb = 1/4 = 2/8
также по т. фалеса:
me/ea = ck/ka = 2/1
раз ме/ев = 2/8
а ме/еа = 2/1, то ев/еа = 8/1, то есть еа составляет 1/7 часть от ав
ea = ab/7 = a/7
cl/lb = 1/4, значит lb составляет 4/5 от св
lb = 4cb/5 = 4a/5
теперь найдем el по т. косинусов :
eb = ea + ab = a/7 + a = 8a/7
lb = 4a/5
el^2 = eb^2 + lb^2 - 2*eb* lb cos (
el^2 = 64a^2/49 + 16a^2/25 - 2* 8a/7 * 4a/5 * 1/2
el^2 = 64a^2/49 + 16a^2/25 - 32a^2/35
el^2 = 1600a^2/1225 + 784a^2/1225 - 1120a^2/1225
el^2 = (1600a^2 + 784a^2 - 1120a^2)/1225
el^2 = 1264a^2/1225
el = √(1264a^2/1225) = 4a(√79)/35
объяснение:
поставь лучший ответ