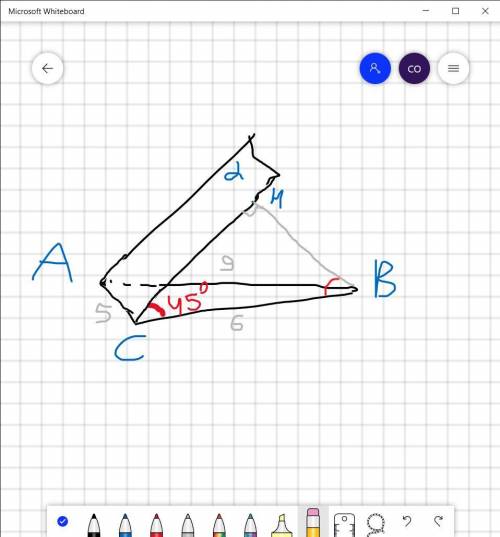
Дано: ΔABC
<(α,ABC)=45°
AB=9см ;BC = 6 см; AC = 5 см
α∩ABC =AC
BH⊥α
Знайти: BH
Розв'язання
ВС-похила до площини α, а ВН-перпендикуляр (оскільки відстань від точки до площини це перпендикуляр проведений із неї до цієї площини), тоді НС-проєкція.
Отже, проєкція похилої НС до площини трикутника ΔABC лежить на відрізку СВ => <HCB=<(α,ABC)=45°
Отримуємо прямокутний трикутник ΔВНС із прямим кутом <СНВ.
Знайдемо невідомий кут <НВС=90°-<HCB=90°-45°=45°
<HCB=<НВС, отже трикутник ΔВНС рівнобедрений і позначимо рівні сторони НС=НВ=х
За теоремою Піфагора
НС²+НВ²=СВ²
х²+х²=6²
2х²=36 | : 2
x²=18
x₁= -√18 (сторонній корень)
х₂=√18=√(9*2)=3√2 см
Відповідь: 3√2 см
(сподіваюся, що правильно)
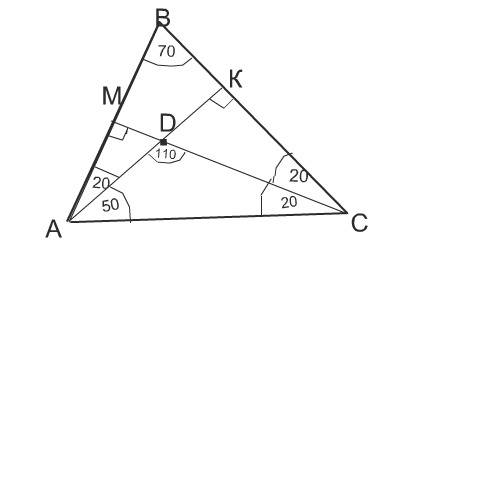
Нарисуем треугольник АВС.
Проведем в нем высоты АК и СМ.
По условию задачи они пересекаются под углом 110º.
1) Рассмотрим треугольник АМС.
Угол АМС =90º
Сумма острых углов в нем 90º, ∠А=70º по условию, следовательно,
∠ МСА=90º-70º=20º.
2)Рассмотрим треугольник АDС.
Так как ∠МСА=20 градусов,
то ∠DAC=180-110-20=50º.
3)Так как ∠ А=70º, а
∠КАС=50º,то ∠ВАК=70-50-20º
4)В прямоугольном треугольнике АВК ∠АКВ прямой, ∠ВАК=20º, следовательно, ∠В=90-20=70º
5) В треугольнике АВС ∠С=180-70-70=40º
ответ: Угол С=40º
1)
AB║A₁B₁║D₁C₁║DC; AD ║BC ║B₁C₁║A₁D₁; AA₁║BB₁║CC₁║DD₁
2)
AA₁ ⊥ AB,A₁B₁ ,A₁D₁ ,AD
BB₁ ⊥ BA,B₁A₁ ,B₁C₁ ,BC
CC₁ ⊥ CB,C₁B₁ ,C₁D₁ ,CD
DD₁ ⊥ DA,D₁A₁ ,D₁C₁ ,DC
3)
AA₁ /· BC,B₁C₁ ,D₁C₁ ,DC
BB₁ /· AD,A₁D₁ ,C₁D₁ ,CD
CC₁ /· BA,B₁A₁ ,D₁A₁ ,DA
DD₁ /· AB,A₁B₁ ,C₁B₁ ,CB
4)
(ABC)║(A₁B₁C₁ ); (ABB₁ )║(DCC₁ ); (BCC₁ )║(ADD₁ )
5)
(ABB₁ ) ⊥ (ABC),(BB₁C₁ ),(B₁A₁D₁ ),(A₁AD)
(DCC₁ ) ⊥ (DCB),(CC₁B₁ ),(C₁D₁A₁ ),(D₁DA)
(BCC₁ ) ⊥ (BCD),(B₁C₁D₁ )
(ADD₁ ) ⊥ (ADC),(A₁D₁C₁ )