1. Построила на рисунке. Масштаб фотографии разный у всех, я взяла длину основания 4см и длину биссектрисы 3см. Свойством пользовалась тем, что в равнобедренном треугольнике биссектриса, проведённая к основанию, является его медианой. Построила медиану по алгоритму построения середины отрезка.
2. Треугольник равнобедренный, т.к. ВО⊥АС, угол АВО=СВО, АО=ОС. Можно измерить сторону и биссектрису. Всё соблюдается.
3. Задача будет иметь решение в том случае, если при построении сумма двух любых сторон треугольника будет больше длины третьей стороны. Т.е. основание не должно быть дано длиннее, чем сумма боковых сторон.
Объяснение:
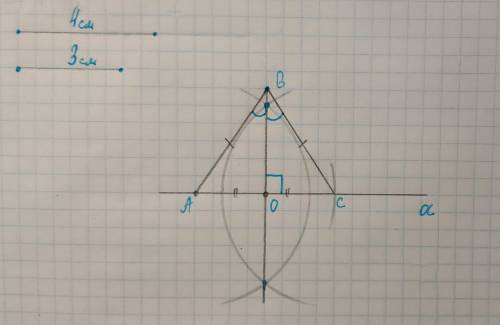
1. Так как треугольник равнобедренный, в нем высота, проведенная к основанию, является и биссектрисой, и медианой. Значит нам необходимо восстановить серединный перпендикуляр к основанию "а" и на нем отложить отрезок, равный длине биссектрисы "b". Соединив уонцы отрезка "а" с точкой конца отрезка "b" на серединном перпендикуляре, получим искомый треугольник.
2. На произвольной прямой откладываем циркулем отрезок АВ, равный данному отрезку "а". Из концов этого отрезка, как из центров, проводим окружности, радиусом больше половины отрезка "а". Соединив точки пересечения окружносткй, получаем серединный перпендикуляр к основанию "а". Откладываем на нем от основания отрезок, равный отрезку "b". Получаем точку С. Соединяем точки А и С, В и С => получаем искомый треугольник.
3. Треугольник равнобедренный, так как любая точка на серединном перпендикуляре равноудалена от концов отрезка, к которому провелен этот перпендикуляр. То есть АС = ВС. Основание этого треугольниеа равно "а", высоты = биссектриса = медиана = "b" по построению.
3. Задача имеет два решения, симметричных относительно прямой "а", независимо от значения отрезков "а" и "b".
