1) BM≈10
2)cosα=0
Объяснение:
1)Дано трикутник ABC
A(0;-3;-1)
B(-4;0;2)
С(8;3;-7)
BM-медіанна
AC(8-0;3-(-3);-7-(-1)) AC(8;6;-6)
М-середина AC
M(8/2;6/2;-6/2) M(4;3;-3)
BM(4-(-4);3-0;-3-2) BM(8;3;-5)
|BM|=√(8²+3²+(-5)²)=√(64+9+25)≈10
2)M(0;1;-1) B(1;-1;2) C(3;1;0) D(2;1;1)
MD(2-0;1-1;1-(-1)) MD(2;0;2)
BC(3-1;1-(-1);0-2) BC(2;2;-2)
Знайдемо скалярний добуток векторів:
MD·BC=2·2+02+2·(-2)=4+0-4=0
Знайдемо довжини векторів:
|MD|=√(2²+0²+2²)=√(4+0+4)=√8=2√2
|BC|=√(2²+2²+(-2)²)=√(4+4+4)=√12=2√3
Знайдемо кут між векторами:
cosα=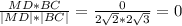
Построить прямоугольный треугольник по данному катету и прилежащему острому углу.
* * *
Пусть данный катет АС, угол - А
На произвольной прямой m отложим отрезок, равный длине катета АС.
Обозначим его концы А и С.
На сторонах заданного угла А циркулем радиуса=АС с центром в т.А сделаем насечки. Обозначим их О и М.
Соединим О и М.
Из т. А построенного на m катета проведем тем же раствором циркуля полуокружность.
Циркулем измерим ОМ и из т.С отложим полуокружность до пересечения с первой в т.К.
АС=АМ, АК=АО, отрезок СК равен отрезку ОМ, ⇒ ∆ АКС=∆ АОМ. Следовательно, угол КАС равен заданному.
Катет и прилежащий к нему угол построены.
На равном расстоянии по обе стороны от С отметим на прямой m т.1 и т.2.
Из этих точек, как из центров, начертим полуокружности так, чтобы они пересеклись по обе стороны от прямой m.
Точки пересечения соединим. Построен перпендикуляр к прямой m через т. С ( это стандартный построения перпендикуляра, и он наверняка Вам знаком).
Точку пересечения перпендикуляра с другой стороной угла А обозначим В.
Искомый треугольник АВС по катету АС и прилежащему углу А построен.
Площадь поверхности шара: Sш=4πR²=4π·50=200π.
Площадь сечения: Sc=πr².
Sш=8·Sc,
200π=8πr² ⇒ r²=200π/8π=25.
В прямоугольном тр-ке АОС ОС²=АО²-АС²=50-25=25,
ОС=5 см - это ответ.