ответ: V=64√5см³
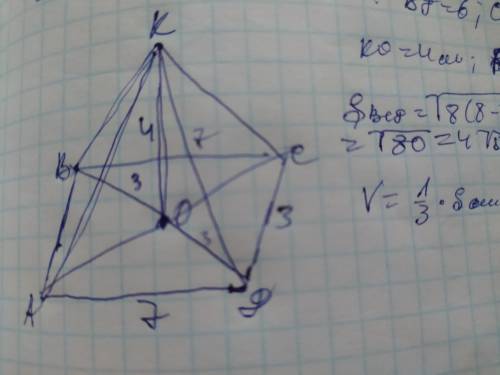
Объяснение: обозначим вершины пирамиды АВСД с высотой КО и диагоналями ВД и АС. Одна диагональ делит параллелограмм на 2 равных треугольника. Пусть ВД=6см. Рассмотрим полученный ∆ВСД. В нём известны 3 стороны и мы можем найти его площадь по формуле: S=√((p-a)(p-b)(p-c)), где а сторона треугольника а р-полупериметр:
Р=3+7+6=16см; р/2=16/2=8см
S=√8((8-7)(8-6)(8-3))=√(8×1×2×5)=
=√80=8√5см²
Так как таких треугольников 2, то площадь параллелограмма=8√5×2=16√5см²
Теперь найдём объем пирамиды зная площадь основания и высоту по формуле: V=⅓×Sосн×КО=
=⅓×16√5×4=64√5/3см³
7
Объяснение:
Точка D проецируется в центр описанной окружности треугольника АСВ -О, так как AD=BD=CD.
То есть ОА=ОВ=ОС= sqrt(25^2-24^2)=7
Таким образом получили 3 равнобедренных треугольника:
АОВ , ВОС ,АОС , в которых бдут равны углы при основании соответственно:
ОАВ=ОВА=а , ОВС=ОСВ=с и ОАС=ОСА=b.
Тогда угол А треугольника АВС= a+b, B=a+c, C=b+c
A+B+C =2a+2b+2c=180 град
=> a+b+c=90 град
Но по условию задачи С= b+c =30 градусов
Значит а=90-30=60 градусов
Отсюда следует, что треугольник АОВ равносторонний и ОА=ОВ=АВ=7
При пересечении двух прямых образуются 4 угла. Если хотя бы один из них=90°, остальные 3 тоже равны 90°.
Если они не равны 90°, то образуется 2 пары вертикальных равных углов: острые ∠2 и ∠4, и тупые ∠1 и ∠3.
Сумма двух тупых углов не может быть равна 126°. Значит, ∠2+∠4=126°. ∠2=∠4=126°:2=63°
Тогда смежные с ними ∠1 и ∠3 равны 180°-63°=117° каждый.