1.
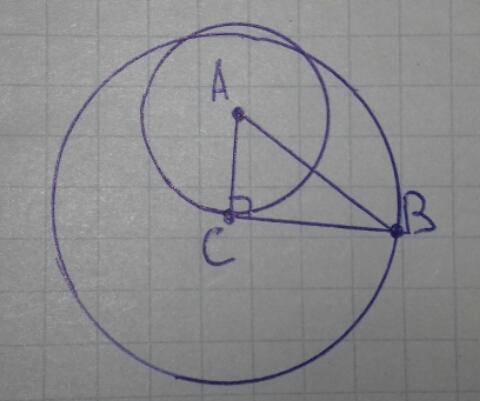
BC⊥AC как катеты прямоугольного треугольника.
BC∩AC = C; AC - радиус окружности с центром A.
Получаем, что BC перпендикулярно радиусу (AC) окружности с центром A и BC пересекает этот радиус в точке (C), принадлежащей той же окружности, поэтому BC это касательная.
2.
AB пересекает окружность (C, CB) в точке B, а CB это радиус той же окружности, проведёный к точке B. Если AB было бы касательной, то AB⊥BC, но это не возможно т.к. AB - гипотенуза, а BC - катет одного прямоугольного ΔABC. Поэтому AB не может быть касательной.
соs а=ае/ав=3/7
ае=(3/7)*ав
ав=7*ае/3
тк ав=вс и ае=се то вс=7*ае/3= 7*се/3
соs с=се/вс=соs а=3/7
sin с=ве/вс
ве=sin с *с
ве=sinс *(7*ае/3)
sin а=ск/ас
ск=sin а*ас
ас=2ае
ск=sin а* 2ае
sin а=sin с
ск/ве=(sin а*2ае)/(sin с*(7ае/3))=2*3/7=6/7
ответ: ск:ве=6/7