Решением треугольника называется нахождение всех его шести элементов (т. е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Из суммы углов треугольника найдем угол С:
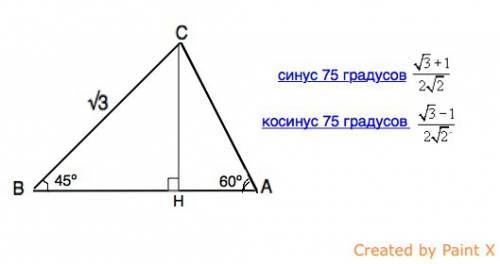
∠С=180º-45º-60º=75º
В прямоугольном ⊿ ВНС угол ВСН=90º-45º=45º
⊿ ВНС - равнобедренный, СН=ВН=ВС•sin 45º=(√3•√2):2
В ⊿ АНС сторона АС=СH:sin 60º
AC=[(√3•√2):2]:(√2):2=√2
АВ=ВН+АН
АН противолежит углу НСА, равному 90º-60º=30º
АН=АС:2=(√2):2
АВ=(√3•√2):2+(√2):2=(√3+1):√2
––––––––––––
Или по т. синусов:
АВ:sin75=BC:sin60
sin 60º=(√3):2
sin 75º=(√3+1):2√2 ( из таблицы тригонометрических функций)
АВ:(√3+1):2√2=(√3):[(√3):2]⇒
AB=(√3+1):√2
--------------
или по т.косинусов
AB²=BC²+AC²- 2BC•AC•cos75º
cos 75º=(√3-1):2√2
AB²=3+2- 2√6•((√3-1):2√2)⇒
AB=√(2+√3)
Оба найденных значения АВ равны - проверьте, возведя их в квадрат.
[√(2+√3)]²=[(√3+1):√2]²
h² = x*y
высота h
гипотенуза 4h
один отрезок x
второй отрезок (4h-x)
h² = x*(4h-x)
h² = 4h*x - x²
x² - 4h*x + h² = 0
D=16h²-4h² = 12h²
x₁;₂ = (4h+-2√3*h)/2 = h*(2 +- √3)
отрезки гипотенузы получились: один = h*(2+√3), другой = h*(2-√3)
отрезки гипотенузы будут ПРИлежащими катетами к острым углам прямоугольного треугольника,
а высота --ПРОтиволежащим к ним катетом
tg(α) = h / (h*(2+√3)) = 1/(2+√3) = 2-√3
tg(β) = h / (h*(2-√3)) = 1/(2-√3) = 2+√3
α = 15°
β = 75°
можно проще)))
любой прямоугольный треугольник можно достроить до прямоугольника, у прямоугольника диагонали равны и точкой пересечения делятся пополам...
получим равнобедренные треугольники с боковыми сторонами по 2h
и в одном из них высота =h, т.е. угол между диагоналями будет =30°, т.к. получим катет, равный половине гипотенузы)))
тогда углы при основании равнобедренного треугольника = (180°-30°)/2 = 75°,
а это и есть острый угол данного прямоугольного треугольника...
второй вычислить уже просто))