Боковая сторона равна 4,15 см
Объяснение:
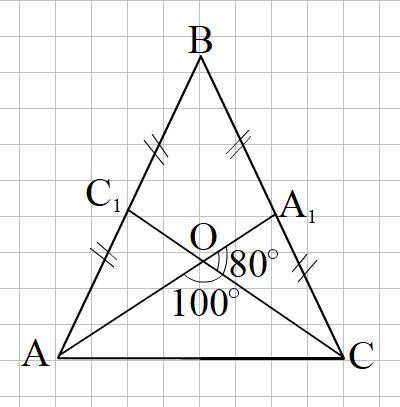
Смотри прикреплённый рисунок.
ΔАА₁В = ΔСС₁В по 1-му признаку равенства треугольников (АВ = ВС как боковые стороны равнобедренного треугольника, ВА₁ = ВС₁ как половинки равных боковых сторон треугольника и ∠В - общий угол)
Тогда медианы АА₁ = СС₁ = 3см
По свойству медиан треугольника АА₁ и СС₁ точкой пересечения О делятся в отношении 2 : 1, считая от вершины. Поэтому
А₁О = 1см, а ОС = 2см.
По свойству смежных углов ∠COА₁ = 180° - ∠АОС = 180° - 100° = 80°
В Δ СОА₁ по теореме косинусов можно найти половину боковой стороны СА₁
СА₁² = А₁О² + ОС² - 2 · А₁О · ОС · cos 80°
СА₁² = 1² + 2² - 2 · 1 · 2 · 0,1736 = 4,3054
СА₁ = √4,3054 = 2,075 (см)
ВС = 2 · СА₁ = 2 · 2,075 = 4,15 (см)
Обозначим параллелепипед АВСДА1В1С1Д1. АВ=6, ВС=13,АА1=8. Плоскость сечения проходит через ВС и точку пересечения диагоналей(центр параллелепипеда). Обозначим её О. Из точки О проведём прямые к стороне основания ОВ и ОС, по условию ВОС лежит в заданной плоскости. Продолжим две пересекающиеся прямые ВО и ОС(диагонали) до их пересечения в т.А1 и Д1. Соединим А1 и В, и Д1 и С. Отрезки А1В и Д1С-проекции диагоналей на боковые грани . То есть в сечении получим прямоугольник А1ВСД1. Одна его сторона ВС другая А1В. А1В=корень из(АВ квадрат+АА1квадрат)=корень из (36+64)=10. Отсюда площадь сечения S= А1В*ВС=10*13=130.
2х-17=180
Х=81,5- первый угол
У угол: 180-81,5=98,5