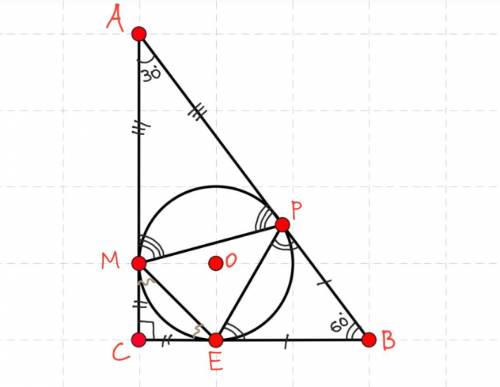
Дано: ΔABC — прямокутний (∠С=90°), ∠А=30°; коло, впис. у ΔABC; М, Р, Е — точки дотику,.
Знайти: ∠ЕМР, ∠МРЕ, ∠РЕМ.
Розв'язання.
Знайдемо третій кут прямокутного трикутника АВС. ∠В= 180°–∠С–∠А= 180°–90°–30°= 60°. (Сума кутів трикутника складає 180°)
1)Існує така властивість: відрізки, проведені з однієї вершини до точок дотику з колом, рівні.
Звідси, АМ=АР, РВ=ВЕ, ЕС=СМ. Це означає, що трикутники МАР, РВЕ і ЕСМ є рівнобедреними.
2) Розглянемо ΔМАР:
АМ=АР => ∠АМР=∠АРМ= (180°–∠А):2= (180°–30°):2= 150°:2= 75°.
3) У ΔРВЕ: ∠В= 60°, РВ=ВЕ => ∠ВРЕ=∠ВЕР= (180°–∠В):2= (180°–60°):2= 60°.
4) У ΔЕСМ: ∠С= 90°, ЕС=СМ => ∠СЕМ=∠СМЕ= (180°–90°):2= 90°:2= 45°.
5) Тепер ми можемо знайти всі кути трикутника МРЕ.
∠ЕМР= 180°–∠СМЕ–∠АМР= 180°–45°–75°= 60°.
∠МРЕ= 180°– ∠АРМ–∠ЕРВ= 180°–75°–60°= 45°.
∠РЕМ= 180°–∠ВЕР–∠СЕМ= 180°–60°–45°= 75°.
Відповідь: 45°, 60°, 75°.
У 2,6 разів, та у 2,8 разів. Два випадки.
Объяснение:
Оскільки це рівнобедрений трикунтник, то дві сторони рівні між собою, а одна відрізняється. Тоді маємо два випадки. Перший, якщо однакові сторони трикутника дорівнюють 4 см, а основа - 5 см. Тоді периметр дорівнює: 4 + 4 + 5 = 13 см. І він більший за основу у: 13/5=2,6 разів.
Другий випадок, якщо однакові сторони трикутника дорівнюють 5 см, а основа - 4 см. Тоді периметр дорівнює: 5 + 5 + 4 = 14 см. І тоді периметр більший за основу у: 14/5=2,8 разів.
1)2а=48
а=24
2)6b=48
b=8
Стороны равны 24см и 8 см