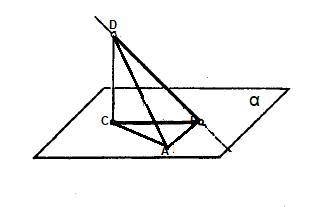
Из точки D, не принадлежащей плоскости α, проведены к этой плоскости перпендикуляр DC и две равные наклонные DA и DB. Известно, что наклонные равны 4 см и ∠CDB=32°. Найдите перпендикуляр DC и проекцию наклонной AC.
Объяснение:
DC-перпендикуляр к плоскости , DA и DB-наклонные, DA=DB=4 см, CA-проекция наклонной DA.
1)ΔDСВ-прямоугольный , т.к. DC⊥α ( значит любой прямой лежащий в этой плоскости)
cos∠CDB=DС/DВ , cos32°=DС/4 ,DС=4cos32° ;
sin∠CDB=CВ/DВ , sin32°=CВ/4 , СВ=4sin32°.
2)ΔDAC=ΔDBC как прямоугольные по катету и гипотенузе:
катет DC-общий, гипотенузы DA=DB поусловию⇒CA=CD=4sin32°.
Дано:
∆MKN. ME - висота (ME ┴ KN). FN - висота (FN ┴ MK).
ME ∩ FN = 0. OM = ON; MF = KE.
Довести: ∆MNK - рівносторонній.
Доведения:
Розглянемо ∆MOF i ∆NOE.
За умовою NF - висота (NF ┴ MK); ∟NFM = 90° i MЕ - висота; ∟MEN = 90°.
1) ∟MFO = ∟NEO = 90°;
2) ∟MOF = ∟NOE (вертикальні);
3) ОМ = ON.
За ознакою piвностi прямокутних трикутників маємо: ∆MFO = ∆NEO.
Звідси MF = EN.
За умовою MF = KE i MF = EN, тобто KE = EN.
За умовою ME - висота. Тоді AMKN - рівнобедрений, MK = MN.
Розглянемо ∆MFN i ∆NEM:
1) ∟MFN = ∟MЕN = 90°;
2) MF = EN;
3) MN - спільна сторона.
Тому ∆MFN = ∆NEM. Звідси ∟FMN = ∟MNE.
Отже, ∆MKN - рівнобедрений. MK = KN. Якщо MK = MN i MK = KN.
Тому ∆ABC - рівносторонній.
Доведено.
Для начала найдём высоту ромба.
S(АВСД)=а²·sinα=8²/2=32 см².
S(АВСД)=a·Н ⇒ Н=S(АВСД)/а=32/8=4 см.
В правильном треугольнике АДК КЕ - высота. КЕ=а√3/2=4√3 см.
Прямые АД и ВС параллельны. Проведём МЕ⊥АД, М∈ВС ⇒ МЕ⊥ВС. МЕ=Н=4 см.
КЕ⊥АД и МЕ⊥ВС, значит по теореме о трёх перпендикулярах КМ⊥ВС, следовательно КМ=4√2 см (по условию).
КЕ⊥АД и МЕ⊥АД, значит ∠КЕМ - линейный угол двугранного угла КАДМ или угол между плоскостями АДК и АВС.
В треугольнике КМЕ по теореме косинусов:
cos∠КЕМ=(КЕ²+МЕ²-КМ²)/(2КЕ·МЕ),
cos∠КЕМ=(48+16-32)/(2·4√3·4)=32/(32√3)=1/√3 - это ответ.