<CAD = 24°.
Объяснение:
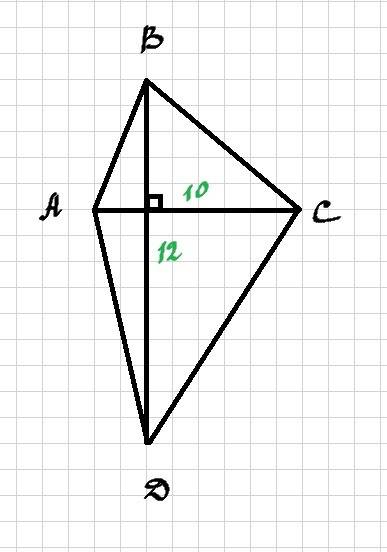
Четырехугольник АВСD - вписанный, так как его диагональ АС является диаметром (углы АВС и ADC равны по 90°, а отрезок АС является общей стороной - гипотенузой треугольников АВС и ADC).
<ADB = <ACB =40°, как вписанные углы, опирающиеся на одну дугу.
<AKB - внешний угол треугольника AKD и равен сумме двух внутреннитх углов, не смежных с ним:
64° = 40° +<CAD => <CAD = 64-40 =24°.
Или так:
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. В нашем случае
<AKB = 64° = полусумме дуг АВ и CD.
Дуга АВ равна 80°, так как на нее опирается вписанный угол АСВ, равный 40°.
Тогда, если сумма дуг АВ и CD = 2*64 = 128°, а дуга АВ = 80°, то дуга CD равна 48°.
Следовательно, <CAD = 24°, как вписанный угол, опирающийся на дугу CD.
ответ: <CAD = 24°.
1) Первый пункт задачи должен быть сформулирован так:
докажите, что все вершины четырехугольника АВСD лежат в одной плоскости, если его диагонали АС и ВD пересекаются.
Воспользуемся теоремой: через две пересекающиеся прямые можно провести плоскость и при том только одну.
Даны две пересекающиеся прямые АС и ВD. Проходящую через них плоскость обозначим α.
Прямая АС лежит в плоскости α, значит А∈α и В∈α.
Прямая ВD лежит в плоскости α, значит В∈α и D∈α.
Точки А, В, С, D принадлежат плоскости α, т.е. все вершины четырехугольника АВСD принадлежат плоскости α.
Что и требовалось доказать.
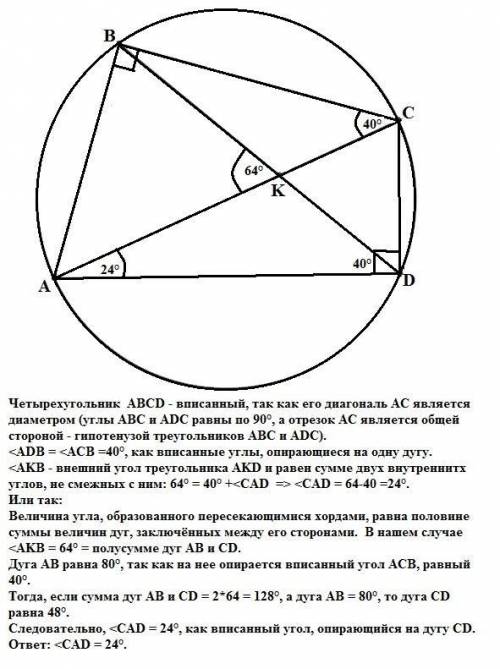
2) Рисунок к задаче прикреплен. Дан четырехугольник, у которого диагонали взаимно перпендикулярны и известны длины этих диагоналей (смотри рисунок).
Воспользуемся формулой для вычисления площади четырехугольника по двум диагоналям и углу между ними.
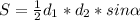 , где
, где 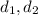 – диагонали четырехугольника,
– диагонали четырехугольника, 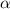 – угол между диагоналями.
– угол между диагоналями.
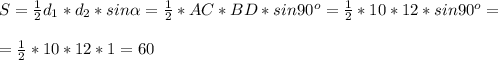
ответ: площадь АВСD равна 60 см².