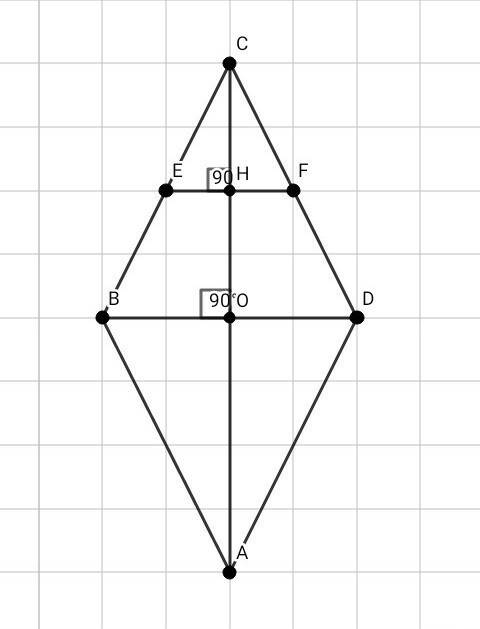
Диагональ делит прямоугольник на два равных прямоугольных треугольника. Рассмотрим ΔАСD (см. прикрепленный рисунок).
АС является гипотенузой в ΔАСD. АС = 3. Также известен острый угол в этом треугольнике ∠CAD = 37°.
Через синус и косинус найдем катеты треугольника АСD.
Синус острого угла в прямоугольном треугольнике - отношение противолежащего катета к гипотенузе.
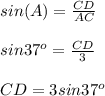
Косинус острого угла в прямоугольном треугольнике - отношение прилежащего катета к гипотенузе.
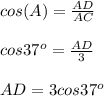
CD и AD являются шириной и длиной в прямоугольника АВСD.
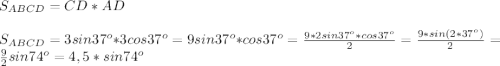
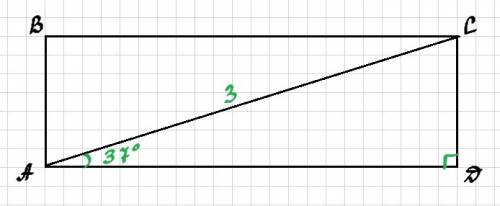
ответ: 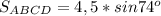 см².
см².
найдем диагональ основания по теореме косинусов:
BD^2=AB^2+BC^2-2AB*BC*cos60=9+25-30*1/2=19...BD=√19
Sсеч=BD*CC1=63
√19*CC1=63
CC1=63/√19
Socn=3*5*√3/2=15√3/2
V=15√3/2*63/√19=945√3/2√19