Задача с неполным условием, имеет бесконечно много решений в зависимости от вида треугольника. Рассмотрим три возможных варианта.
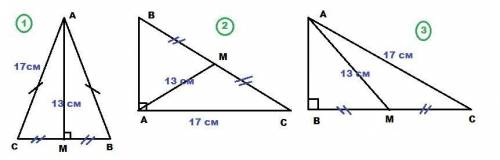
1) ΔABC - равнобедренный, AC = AB; AM=13 см; AC = 17 см
AM - медиана, в равнобедренном треугольнике одновременно высота ⇒ CM = MB; AM⊥CB
ΔAMC - прямоугольный, ∠AMC=90°; AM=13 см; AC = 17 см
Теорема Пифагора :
CM² = AC² - AM² = 17² - 13² = 120 = (2√30)²
CM = 2√30 см
BC = 2 CM = 2 · 2√30 = 4√30 см
BC = 4√30 см
=========================================
2) ΔABC - прямоугольный; ∠BAC = 90°; AM=13 см; AC = 17 см
AM - медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
BC = 2 AM = 2 · 13 = 26 см;
BC = 26 см
====================================
3) ΔABC - прямоугольный, ∠ABC = 90°; AM=13 см; AC = 17 см
AM - медиана ⇒ BM = MC; BC = 2BM
Теорема Пифагора
AB² = AC² - BC² = 17² - (2BM)² = 289 - 4BM²
Теорема Пифагора для ΔABM
AB² = AM² - BM² = 13² - BM² = 169 - BM²
169 - BM² = 280 - 4BM²
3BM² = 111; BM² = 37
BM = √37 см ⇒ BC = 2BM = 2√37 см
BC = 2√37 см
Записываем теорему Пифагора:
(5+x)² + (12+x)² = (5+12)²
Раскрывая скобки, перенося все члены в левую часть и приводя подобные слагаемые, получаем квадратное уравнение:
x² + 17x − 60 = 0
(x−3)(x+20) = 0
x=3 (подходит) или x=−20 (отрицательное значение ⇒ не подходит)
Итак, радиус вписанной окружности равен 3 см, тогда первый катет равен 3+5 = 8 (см) , второй катет: 3+12 = 15 (см) .
ответ 8 и 15