Пошаговое объяснение:Нам известен отрезок на который опирается известный угол. Поэтому легко построить окружность описанную около искомого треугольника (для этого можно , например, на луче заданного угла взять точку из которой засечь на другом луче точку удаленную от первой на расстояние равное данному отрезку, а потом около треугольника описать окружность. Последнее построение -стандартное). Биссектриса делит дугу на которую опирается отрезок пополам. Середина дуги находится как точка пересечения перпендикуляра из середины отрезка с окружностью. Пусть середина дуги точка Е. Строим точку Д делящую отрезок на два заданных. Проводим ЕД до пересечения с окружностью. Точка пересечения - третья вершина искомого треугольника.
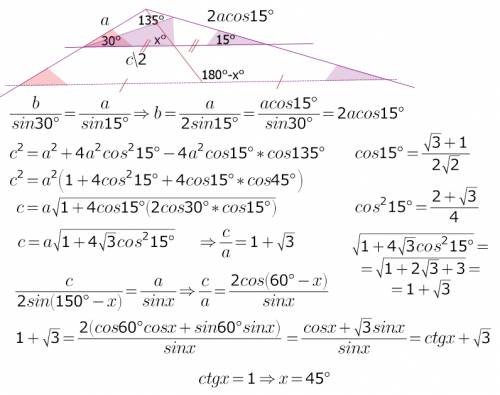
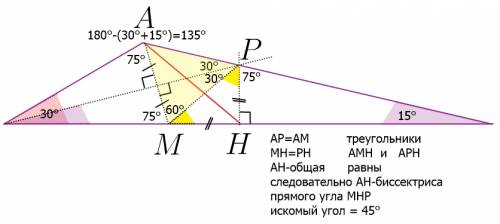
В сечении получим заданный угол α между плоскостью боковой грани правильной треугольной пирамиды и плоскостью её основания и искомый угол β между боковым ребром и плоскостью основания пирамиды.
Обозначим высоту пирамиды х, проекцию апофемы на основание у.
По свойству медианы основания проекция бокового ребра на основание равна 2y.
Тогда tg α = x/y = 5.
tg β = x/(2y) = (1/2)*5 = 2,5.