Длина картона кратна и ширине, и длине карточки:
48:16=3, 48:12=4. Ширина картона НЕ кратна ни длине, ни ширине карточки.
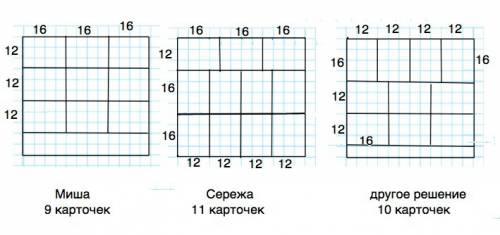
По ширине нужно разметить первую линию разреза так, чтобы оставшаяся часть картона по ширине была кратна одному из размеров карточки.
Если отрезать первую полосу шириной 16 см, ширина оставшейся части картона будет 28 - не кратна ни одному размеру карточки.
Следовательно, сначала нужно отрезать от картона полоску шириной в 12 см и разрезать на 3 части.
Оставшийся лист будет размером 32•48, и оба его размера теперь кратны длине карточки. Разрезав его по ширине на две полоски по 16 см, можно затем каждую разрезать на 4 карточки шириной 12 см, при этом излишков не образуется.
Если первую полоску отрезать шириной 16 см, ширина оставшейся части картона не будет кратной ни длине, ни ширине. Поэтому ее нельзя будет разрезать, чтобы не осталось лишнего картона.
Данный лист картона можно разрезать на 11 карточек, при этом не образуется излишков.
30 см
Объяснение:
Рассмотрим вложение.
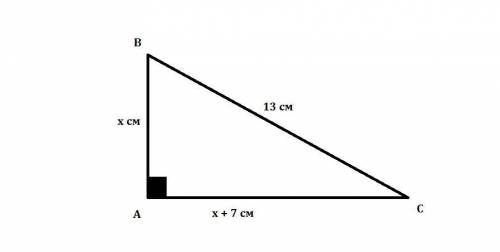
Нам дан ΔАВС: ∠А = 90°, ВС = 13 см
Пусть АВ = х см, тогда АС = х + 7 см. Воспользуемся т.Пифагора для нахождения стороны.
АВ² + АС² = ВС²
х² + (х + 7)² = 13²
х² + х² + 14х + 49 = 169
2х² + 14х + 49 - 169 = 0
2х² + 14х - 120 = 0 |:2
х² + 7х - 60 = 0
D = 7² - 4 * (-60) = 49 + 240 = 289 = 17²
x₁ = (-7 - 17)/2 = -24/2 = -12
x₂ = (-7 + 17)/2 = 10/2 = 5
т.к. сторона не может быть отрицательна, то АВ = 5 см, тогда
АС = 5 + 7 = 12 см
Чтобы найти периметр треугольника, надо сложить все стороны.
Р = АВ + ВС + АС = 5 + 13 + 12 = 30 см
ΔСВН - прямоугольный с углом В = 60°. В этом треугольнике угол СНВ = 90°, следовательно угол ВСН = 30°.
Биссектриса СР делит прямой угол С пополам, поэтому ВСР = 45°.
Искомый угол между биссектрисой и высотой ∠НСР = ∠ВСР - ∠ВСН =45° - 30° = 15°
ответ: 15°