Один из углов параллелограмма равен 56°. найти все его углы. и если можно с чертежом.

👇

Ответ:

oksana1382

05.01.2021

У параллелограмма есть свойства, одно из которых, это то, что - противоположные углы пар-ма равны.
в задание дано, один из углов пар-ма равен 56° ⇒ противоположный угол будет равен также 56°. (см. приложение).
далее, когда мы знаем два угла пар-ма, мы можем найти и остальные
углы. ⇒ 360° - (56°+56°) = 248°
далее, мы уже знаем, что противоположные углы пар-ма равны, ⇒ 248 : 2 = 124°
ответ:
∡А = 56°
∡В = 124°
∡С = 56°
∡D = 124°

Один из углов параллелограмма равен 56°. найти все его углы. и если можно с чертежом.

Один из углов параллелограмма равен 56°. найти все его углы. и если можно с чертежом.

4,4(62 оценок)

Открыть все ответы

Ответ:

стефания31

05.01.2021

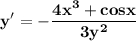
1. $\displaystyle \bf y'=-\frac{4x^3+cosx}{3y^2}$

2. $\displaystyle \bf y'(x)=-\frac{2}{t^2cost}$

3. $\displaystyle \bf y_k=-0,06x+0,72$ ;

$\displaystyle \bf y_n=\frac{50}{3}x+50,9$ .

Объяснение:

1. Найти производную функции у(х), которая задана неявно уравнением:

$\displaystyle x^4+y^3+sinx=0$

Так как у является функцией от х, то будем рассматривать у³ как сложную функцию от х.

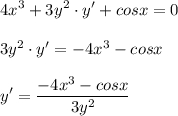
$\displaystyle 4x^3+3y^2\cdot y'+cosx=03y^2\cdot y'=-4x^3-cosxy'=\frac{-4x^3-cosx}{3y^2}$

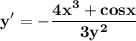
$\displaystyle \bf y'=-\frac{4x^3+cosx}{3y^2}$

2. Найдите производную функции y (x), заданную параметрически.

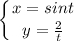
$\displaystyle \left \{ {{x=sint} \atop {y=\frac{2}{t} }} \right.$

Формула производной для функции, заданной параметрически:

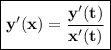
$\boxed {\displaystyle \bf y'(x)=\frac{y'(t)}{x'(t)} }$

Найдем x'(t) и y'(t):

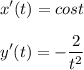
$\displaystyle x'(t)=cost\\ \\ y'(t)=-\frac{2}{t^2}$

$\displaystyle \bf y'(x)=-\frac{2}{t^2cost}$

3. Найти уравнение касательной и нормали к графику функции y= f(x) в точке абсциссой x₀.

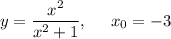
$\displaystyle y=\frac{x^2}{x^2+1} ,\;\;\;\;\;x_0=-3$

Найдем производную:

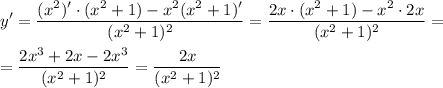
$\displaystyle y'=\frac{(x^2)'\cdot (x^2+1)-x^2\vdot(x^2+1)'}{(x^2+1)^2} =\frac{2x\cdot(x^2+1)-x^2\cdot 2x}{(x^2+1)^2} ==\frac{2x^3+2x-2x^3}{(x^2+1)^2} =\frac{2x}{(x^2+1)^2}$

Найдем значение функции и ее производной в точке x₀ = -3.

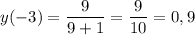
$\displaystyle y(-3)=\frac{9}{9+1 }=\frac{9}{10}=0,9$

$\displaystyle y'(-3)=\frac{-6}{(9+1)^2}=-\frac{6}{100} =-0,06$

Уравнение касательной:

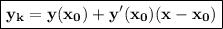
$\boxed {\displaystyle \bf y_k=y(x_0)+y'(x_0)(x-x_0)}$

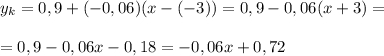
$\displaystyle y_k=0,9+(-0,06)(x-(-3))=0,9-0,06(x+3)=\\ \\=0,9-0,06x-0,18=-0,06x+0,72$

Получили уравнение касательной:

$\displaystyle \bf y_k=-0,06x+0,72$

Уравнение нормали:

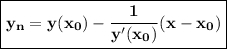
$\boxed {\displaystyle \bf y_n=y(x_0)-\frac{1}{y'(x_0)} (x-x_0)}$

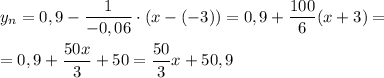
$\displaystyle y_n=0,9-\frac{1}{-0,06} \cdot(x-(-3))=0,9+\frac{100}{6} (x+3)==0,9+\frac{50x}{3} +50=\frac{50}{3}x+50,9$

Получили уравнение нормали:

$\displaystyle \bf y_n=\frac{50}{3}x+50,9$

#SPJ1

4,8(56 оценок)

Ответ:

MadiHale

05.01.2021

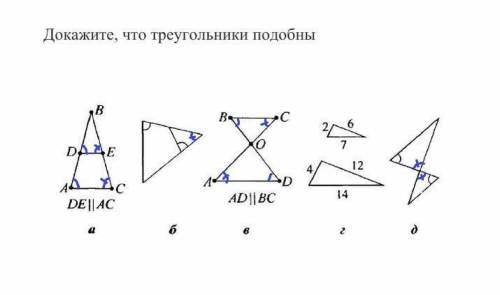
а) ∠BDE=∠BAC и ∠BED=∠BCA (как соответственные углы), значит треугольники BDE и BAC подобны по двум углам

б) Углы, отмеченные на рисунке черным цветом, равны по условию. Также у треугольников имеется общий угол (см. приложенный рисунок), значит большой и маленький треугольник подобны по двум углам

в) ∠CBO=∠ODA и ∠BCO=∠OAD (как накрест лежащие углы), значит треугольники BCO и OAD подобны по двум углам

г) Треугольники подобны по двум сторонам: 2/4=6/12=7/14

д) Углы, отмеченные на рисунке черным цветом, равны по условию. Углы, отмеченные синим (см. приложенный рисунок) равны, так как являются вертикальными. Получается, треугольники подобны по двум углам