Нужно ! в основании пирамиды лежит прямоугольный треугольник с катетом а и прилежащим острым углом бета. определите объем пирамиды если все боковые ребра пирамиды наклонены к её основанию под углом альфа

👇

Ответ:

store1488

24.03.2020

В основании пирамиды лежит прямоугольный треугольник с катетом а и прилежащим острым углом бета. определите объем пирамиды если все боковые ребра пирамиды наклонены к её основанию под углом альфа

Решение в приложении
Нужно ! в основании пирамиды лежит прямоугольный треугольник с катетом а и прилежащим острым углом б

Нужно ! в основании пирамиды лежит прямоугольный треугольник с катетом а и прилежащим острым углом б

4,4(100 оценок)

Открыть все ответы

Ответ:

карольчик1

24.03.2020

Объяснение:

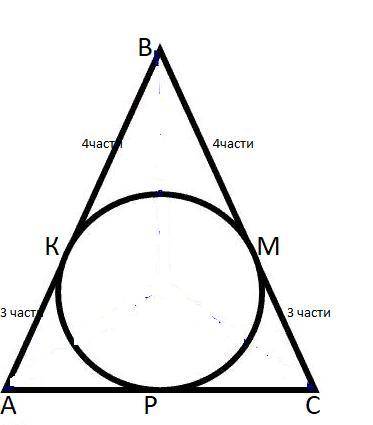
Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 3;4,считая от вершины угла при основании треугольника.Найдите боковую сторону треугольника,если его основание равно 12 см.

Пусть К, М, Р- точки касания соответственно сторн АВ,ВС,АС.

Пусть одна часть х см, тогда Ак=3х, КВ=4х.

Т.к треугольник равнобедренный , то СМ=3х,

По свойству отрезков касательных АК=АР=3х, СМ=СР=3х.

АС=3х+3х=6х и АС=12 см ⇒ значит 6х=12, х=2

АВ=3х+4х =7х ,

АВ=14 см

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении

4,7(59 оценок)

Ответ:

радмирик

24.03.2020

На прямой "а" откладываем данный нам отрезок АЕ - биссектрису.
Строим угол А треугольника. Для этого проводим окружность с центром в вершине А ДАННОГО нам угла произвольного (не очень большого) радиуса. Получаем "засечки" - точки G и F на сторонах данного нам угла.
На прямой "а" чертим окружность с центром в точке А радиусом АG.
Чертим окружность с центром в полученной точке G (пересечение окружности с прямой "а") радиусом GF.
В точеке пересечения двух окружностей получаем точку F. Через точки А и F проводим прямую - получили первую сторону угла А.
Поскольку АЕ - биссектриса, проводим прямую АО через точки А и вторую точку пересечения двух окружностей - точку F1. Получили угол ВАО при вершине А искомого треугольника, равного величине УДВОЕННОГО данного нам угла.
В точке О на прямой АО строим угол, равный углу ВАО, но "зеркальный" ему. Для этого проводим окружность с центром в точке О радиусом АG.
Чертим окружность с центром в полученной точке M (пересечение окружности с прямой AO) радиусом F1F.
В точке пересечения двух окружностей получаем точку N. Через точки O и N проводим прямую - получили вторую сторону угла АОN, равного углу ВАО.
Теперь через точку Е проводим прямую, параллельную прямой ОN.
В точках пересечения этой прямой с прямыми АО и АF получаем вершины искомого треугольника С и В.
Требуемый треугольник построен.

P.S. Построение прямой, параллельной данной ОN, проходящей через точку Е:
1. Проводим окружность с центром в точке N радиусом NE.
2. На прямой ON в месте пересечения с этой окружностью ставим
точку Р.
3. Проводим окружность с центром в точке Р радиусом NE.
4. Проводим окружность с центром в точке Е радиусом NE. На пересечении этой и предыдущей окружностей получаем точку Q.
5. Через точки Е и Q проводим прямую ЕQ. Это и будет прямая, параллельная прямой ON.

Постройте равнобедренный треугольник по биссектрисе треугольника,проведённой из вершины угла при осн