Площадь трапеции равна 900√3 м²
Объяснение:
Дано:
ABCD - трапеция
АС - диагональ трапеции
AB = CD - боковые стороны
АС ⊥ CD
AD = 40√3 м - большее основание
∠A = ∠D = 60°
Найти:
S - площадь трапеции
Рассмотрим прямоугольный треугольник ACD, гипотенуза которого AD = 40√3 м и ∠D = 60°.
Катеты АС и CD этого треугольника равны
АC = AD · sin 60° = 40√3 · 0.5√3 = 60 (м)
CD = AD · cos 60° = 40√3 · 0.5 = 20√3 (м)
Поскольку трапеция равнобедренная, то
АВ = CD = 20√3 м.
Из вершины С прямого угла треугольника ACD опустим на гипотенузу AD высоту CK, которая одновременно является и высотой трапеции
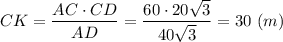
В треугольнике ACD
∠CAD = 90° - ∠D = 90° - 60° = 30°
Основания трапеции ВС ║ АD
∠ACB = ∠CAD = 30° (внутренние накрест лежащие углы при ВС ║ АD и секущей АС).
Рассмотрим ΔАВС.
∠ВАС = ∠BАD - ∠CAD = 60° - 30° = 30°
Поскольку в ΔАВС углы ∠ВАС = ∠ACB = 30°, то ΔАВС - равнобедренный, то есть ВС = АВ = 20√3 м.
Площадь трапеции равна произведению полусуммы оснований на высоту.
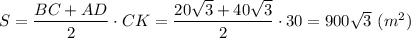
1) Я эту букву по середине не понял так что будет O
ABO = DOC, по двум сторонам и углу между ними, стороны равны по условию, а углы вертикальные;
4) BCD = ABD, по двум сторонам и углу между ними, одна сторона и угол равны по условию, а сторона BD общая;
7) NPK = MNK, по трём сторонам, две равны по условию, третья общая;
10) Треугольник ABC равнобедренный, это следует из условия, обозначим точку пересечения отрезков AD и BE как точку O. Треугольник ABO равнобедренный так как уголки данные из задания равны то и большие углы CBA и CAB равны то есть и углы OBA и OAB равны. Из этого следует что стороны AO и BO равны.
BDO и AOE равны по стороне и двум углам прилежащим к ней, один угол равен по условию, второй вертикальный, а сторону мы доказали.
Объяснение:
a=12
b=4x
c=5x
c²=b²+a²⇒(5x)²=(4x)²+12²
25x²=16x²+144
25x²-16x²=144
9x²=144
x²=16
x=√16
x=4
c=5*4=20
R=20/2=10
ответ 10