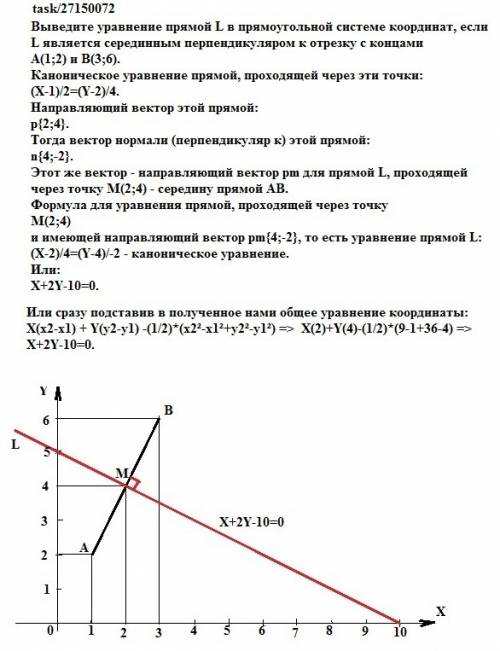
Пускай нам дан прямоугольный треугольник АВС пункт О - середина гипотенузы АС докажим, что АО = ОВ = ОС
Доказательство: проводим в треугольнике АОВ высоту ОН, <AHO = <CBA ==> HO II BC а раз О - середина АС, то НО - средняя линия ==> АН = HB и значит ДАОВ - равнобедренный (НО - медиана и высота) ==> AO = OB проводим в треугольнике ВОС высоту ОН1, <OH1C = <CBA ==> H10 II BA а раз О - середина АС, Н10 - средняя линия ==> BH1 = H1C и значит
- равнобедренный (Н10 - медиана и высота) ==> ОВ = ОС
и значит = OC = BO
AK=(-1-2:4-4)=(-3;0)
AK=√(-3)²+0²=3