Сложность в том, что у меня нет возможности построить эту пирамиду, но поскольку тут проверяется масса формул, попробую объяснить без рисунка. Объем пирамиды равен произведению трети площади основания на высоту. Площадь основания - площадь правильного треугольника, равна а²√3/4, чтобы найти сторону основания а, надо связать ее формулой с радиусом вписанной в основание окружности, а₃=2r*tg(180°/3)=2r*tg60°=2r*√3, и тогда площадь основания 4*r²*3√3/4=r²*3√3; высота основания, т.е. высота правильного треугольника равна а₃√3/2=2r*√3*√3/2=3r, а треть высоты равна проекции апофемы на плоскость основания, угол, образованный апофемой и этой проекцией, и есть данный в условии, угол γ, т.к. апофема перпендикулярна стороне основания, то по теореме о трех перпендикулярах и проекция ей перпендикулярна. Треть высоты основания равна 3r/3=r. Чтобы найти высоту пирамиды, надо проекцию апофемы умножить на tgγ, т.е. высота равна r*tgγ.
Объем пирамиды равен r²*3√3*r*tgγ/3=r в кубе √3*tgγ
Дано: пирамида SABC, SH⊥(ABC), SH = 4 см,
∠ASH=∠CSH=∠BSH=45°, ∠ACB=90°, ∠BAC=30°
Найти : Sбок
Решение : так как боковые рёбра образуют с высотой пирамиды равные углы, значит, они образуют равные углы с основанием пирамиды (острые углы прямоугольных треугольников, равных по общему катету и острому углу). ⇒ Высота опускается в центр окружности, описанной около основания пирамиды. Основание пирамиды - прямоугольный треугольник, центр описанной окружности лежит на середине гипотенузы. H ∈ AB, AH = BH.
SH⊥(ABC) ⇒ SH⊥AB ⇒ ∠SHA=90°
ΔSAH - прямоугольный равнобедренный, так как ∠SAH=∠ASH=45° ⇒ AH = SH = 4 см ⇒ AB = AH + BH = 8 см; SA = 4√2 см
SA = SB = SC = 4√2 см
ΔABC - прямоугольный. Катет, лежащий против угла 30°, равен половине гипотенузы. BC = AB/2 = 4 см
По теореме Пифагора
AC² = AB² - BC² = 8² - 4² = 48
AC = √48 = 4√3 см
Площадь двух других граней можно найти по формуле Герона
ΔASC,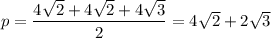
ΔBSC,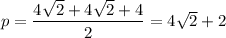
ответ: 4(4 + √15 + √7) см²