На основании ac равнобедренного треугольника abc отметили точки d и e такие,что ad=ce,точка d лежит между точками a и e. докажите,что bd=be решить !

👇

Ответ:

МАВ03022004

25.08.2020

Рассмотрим ΔАВD и ΔBCE:
∠ВАD = ∠ВСЕ (так как углы при основании равнобедренного ΔАВС равны)
АВ = ВС (так как ΔАВС равнобедренный)
AD = CE (по условию)
Следовательно ΔАВD = ΔBCE по двум сторонам и углу между ними.
У равных Δ соответствующие элементы равны, следовательно BD=BE.
Что и требовалось доказать.

На основании ac равнобедренного треугольника abc отметили точки d и e такие,что ad=ce,точка d лежит

На основании ac равнобедренного треугольника abc отметили точки d и e такие,что ad=ce,точка d лежит

4,5(21 оценок)

Открыть все ответы

Ответ:

ЕнотОбормот

25.08.2020

Радиус окружности, описанной около равнобедренного треугольника с углом 120°, равен см. Найдите стороны треугольника

Объяснение:

ΔАВС, ∠В=120°, О-центр описанной окружности. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров к его сторонам.

Пусть ВН⊥АС, О∈ВН., ОВ=ОА=6√3 см.

По теореме синусов( отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности) : 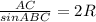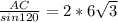$\frac{AC}{sin ABC} =2R$ , $\frac{AC}{sin 120} =2*6\sqrt{3}$ , АС=12√3* 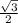$\frac{\sqrt{3} }{2}$ =18 (см).

По свойству высоты равнобедренного треугольника ∠АВН=∠НВС=60°, АН=НС=9 см.

ΔАВН-прямоугольный , sin 60°=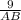 $\frac{9}{AB}$ , АВ=6√3 см ⇒ВС=6√3 см.

4,4(71 оценок)

Ответ:

epoluektova

25.08.2020

См. рис1:

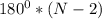
Для вычисления суммы углов выпуклого N-многоугольника нужно использовать формулу 180^0*(N-2)

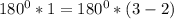
Треугольник ABC состоит из ОДНОГО треугольника, значит сумма всех его углов равна 180^0*1=180^0*(3-2)

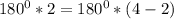
Четырехугольник DEFG состоит из ДВУХ треугольников, значит сумма всех его углов равна 180^0*2=180^0*(4-2)

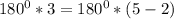
Пятиугольник MNOPQ состоит из ТРЕХ треугольников, значит сумма всех его углов равна 180^0*3=180^0*(5-2)

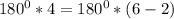
Шестиугольник RSTUVW состоит из ЧЕТЫРЕХ треугольников, значит сумма всех его углов равна 180^0*4=180^0*(6-2)

........

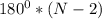N-угольник состоит из N - 2 треугольников, значит сумма всех его углов равна 180^0*(N-2)

(строго доказываеться с метода математической индукции)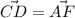
------------------------------------------------

Теперь сама задача см. Рис. 2
По скольку 6-угольник ABCDEF правильный, то $\vec{CD}=\vec{AF}$
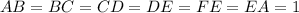
также AB=BC=CD=DE=FE=EA=1

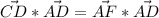Находить скалярное произведение $\vec{CD}*\vec{AD}=\vec{AF}*\vec{AD}$ будем за опредилением через угол: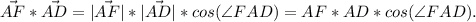
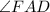$\vec{AF}*\vec{AD}=|\vec{AF}|*|\vec{AD}|*cos(\angle FAD)=AF*AD*cos(\angle FAD).$

Как видим, нам нужно найти величину угла $\angle FAD$ и длину стороны

.

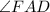(1) $\angle FAD$ :

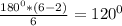
угол правильного 6-угольника равен: $\frac{180^0*(6-2)}{6}=120^0$

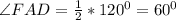
диагональ AD разделяет 6-угольник пополам, и потому угол $\angle FAD=\frac{1}{2}*120^0=60^0$

(2)

:
для нахождения AD найдем сначала DF за теоремой косинусов в треуг. FED:
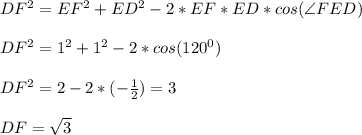
$DF^2=EF^2+ED^2-2*EF*ED*cos(\angle FED)\\\\
DF^2=1^2+1^2-2*cos(120^0)\\\\
DF^2=2-2*(-\frac{1}{2})=3\\\\
DF=\sqrt{3}$

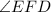
также из треуг. FED найдем угол $\angle EFD$

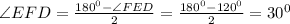
треуг. FED равнобедренный, по этому $\angle EFD=\frac{180^0-\angle FED}{2}=\frac{180^0-120^0}{2}=30^0$

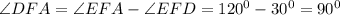
тогда угол $\angle DFA=\angle EFA-\angle EFD=120^0-30^0=90^0$

из треуг. DFA за теор. Пифагора:
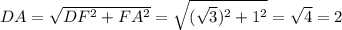
$DA=\sqrt{DF^2+FA^2}=\sqrt{(\sqrt{3})^2+1^2}=\sqrt{4}=2$

------------------------\\
тогда:
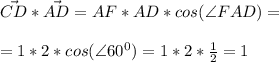
$\vec{CD}*\vec{AD}=AF*AD*cos(\angle FAD)=\\\\
=1*2*cos(\angle 60^0)=1*2*\frac{1}{2}=1$

ответ: 1
Собьяснением! сторона правильного шестиугольника abcdef равняется 1 . и надо посчитать вектор ad*cd