а) ∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 20°,
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 160°.
b) ∠ 1 = ∠ 2 = ∠ 3 = ∠ 4 = ∠ 5 = ∠ 6 = ∠ 7 = ∠ 8 = 90°.
с) ∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 32°,
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 148°.
Объяснение:
Задание а.
∠ 1 = 20°,
тогда ∠ 2 = 180° - ∠ 1 = 180° - 20° = 160°;
∠ 1 = ∠ 4 = 20° - как углы вертикальные;
∠ 1 = ∠ 5 = 20° - как углы соответственные при параллельных прямых а и b и секущей с;
∠ 5 = ∠ 8 = 20° - как углы вертикальные;
таким образом образом,
∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 20°;
аналогично и остальные 4 угла равны между собой:
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 160°.
Задание b.
∠ 1 = ∠ 2 = 180° : 2 = 90°
Согласно доказательству в Задании а):
∠ 1 = ∠ 2 = ∠ 3 = ∠ 4 = ∠ 5 = ∠ 6 = ∠ 7 = ∠ 8 = 90°.
Задание с.
∠ 1 = 32°,
тогда ∠ 2 = 180° - ∠ 1 = 180° - 32° = 148°;
∠ 1 = ∠ 4 = 32° - как углы вертикальные;
∠ 1 = ∠ 5 = 32° - как углы соответственные при параллельных прямых а и b и секущей с;
∠ 5 = ∠ 8 = 32° - как углы вертикальные;
таким образом образом,
∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 32°;
аналогично и остальные 4 угла равны между собой:
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 148°.
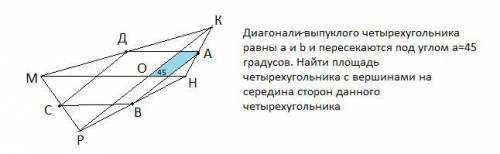
Диагонали выпуклого четырехугольника равны a и b и пересекаются под углом a=45 градусов. Найти площадь четырехугольника с вершинами на середина сторон данного четырехугольника
Объяснение:
МКНР -выпуклый четырехугольник ,МН=а , КР=b ,О-точка пересечения диагоналей , ∠КОН=45°.
Пусть А, В, С, Д-середины сторон. Тогда
АД-средняя линия ΔМВН , АД=1/2*а;
ВС-средняя линия ΔМРН , ВС=1/2*а;
АВ-средняя линия ΔКНР , АВ=1/2*b ;
СД-средняя линия ΔКМР , АВ=1/2*b . Получили , что противоположные стороны попарно равны⇒ АВСД-параллелограмм , по признаку параллелограмма.
S=a*b*sinα , Найдем угол α между сторонами параллелограмма.
Т.к АД║МН , АВ║КР , по свойству средней линии , то синяя фигура на чертеже -параллелограмм, у которой противоположные углы равны⇒∠ДАВ=45°.
S=АД*АВ*sin∠ДАВ =1/2*а*1/2*b*sin45°=1/4*ab*√2/2=(ab√2)/8.
20 см узнавать по тореме пифагора,каждую из диагоналей подели на 2 там получтся у одного прямоугольного треугольника его катет1=12 катет2=16 и по пифагору