ответ: x+y-9=0.
Объяснение:
Для того, чтобы все точки прямой a*x+b*y+c*=0 находились на равном расстоянии от точек А и В, эта прямая должна быть перпендикулярна прямой АВ и проходить через середину отрезка АВ. Пусть точка С - точка пересечения данных прямых; найдём её координаты:
Xc=(Xa+Xb)/2=3; Yc=(Ya+Yb)/2=6. Составим теперь уравнение прямой АВ:
(x-Xa)/(Xb-Xa)=(y-Ya)/(Yb-Ya), или (x-1)/4=(y-4)/4, или y=x+3. Отсюда следует, что угловой коэффициент k1 данной прямой равен k1=1. А так прямая a*x+b*y*c=0 перпендикулярна прямой АВ, то её угловой коэффициент k2=-1/k1=-1. Теперь составим уравнение прямой a*x+b*y*c=0: y-Yc=k2*(x-Xc), или y-6=-1*(x-3), или x+y-9=0.
1.
Получаем 2 прямоугольных треугольника с катетами: х и 5 у первого и 15-х и 5 у второго.
Площадь прямоугольного треугольника равна половине произведения его катетов, т.е. имеем 5х/2 - площадь первого и 5*(15-х)/2 - площадь второго. Сумма площадей этих прямоугольных треугольников искомой равна площади исходного треугольника:
S=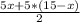
S=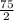
S=37.5
2.
Обозначим неизвестный катет за x. Тогда x=
=
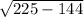=9
S=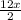
S=12*9/2=54 см²
3.
Площадь ромба равна сумме площадей прямоугольных треугольников, которые он образовывает своими диагоналями. Соответственно, если имеем диагонали 20 и 40, то S одного треугольника=10*20/2=100 см²
S ромба равна 4*100=400 см²
Периметр ромба будет равен сумме 4-х гипотенуз, вышеупомянутых треугольников, а так как они равны, то
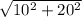P=4*
=4*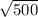
≈4*22.36≈89.44 см²
