 Проведем среднюю линию трапеции; пусть она равна a. Если
Проведем среднюю линию трапеции; пусть она равна a. Если
LN = a+b, то KM=a-b; AD=a+3b; BC=a-3b.
Высоты всех трех трапеций одинаковы; пусть они равны h. Тогда
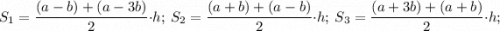
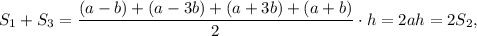
что и требовалось доказать.
А еще проще можно рассуждать так. Проведем средние линии m, n и k верхней, средней и нижней трапеций. Очевидно, что средняя линия средней трапеции является также средней линией трапеции, чьими основаниями служат средние линии верхней и нижней трапеций. Остается вспомнить, что средняя линия трапеции равна полусумме оснований, а также то, что площадь трапеции равна произведению средней линии на высоту. Поэтому площадь верхней трапеции равна mh, площадь нижней трапеции равна kh, площадь средней трапеции равна
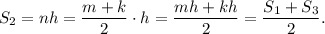
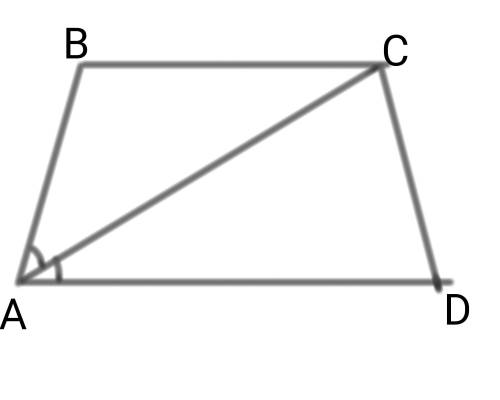
Трапеция равнобедренная AB=CD.
AC=6√3
∠A=60°
В равнобедренной трапеции прилежащие к боковой стороне углы дают в сумме 180°.
∠B=180°-60°=120°
Диагональ по условию делит острый угол ∠А пополам, значит ∠BAC=30°.
Рассмотрим ΔABC:
Сумма внутренних углов треугольника 180°.
∠ABC+∠BAC+∠ACB=180°
120°+30°+∠ACB=180°
∠ACB=30°
Так как ∠ACB=∠BAC, ΔACB – равнобедренный. Значит боковые стороны и меньшее основание равны, AB=CD=BC.
По теореме синусов, стороны пропорциональны синусам противолежащего угла.
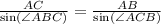
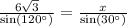
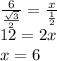
AB=6
Следовательно, AB=BC=CD=6.
∠B=∠C, потому что это равнобедренная трапеция.
∠ACD=∠C-∠ACB
∠ACD=120°-30°=90°
Значит ΔACD – прямоугольный, где угол ∠ACD – прямой.
По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
AD²=AC²+CD²
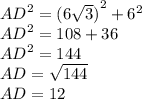
P=AB+BC+CD+AD
P=6+6+6+12=30
Можно также рассмотреть треугольник ABC с длиной стороны AC стремящейся к нулю. Не трудно показать, что в этом случае описанная в условии окружность должна касаться линии AB вблизи стремящейся к нулю окрестности точки B, длина AB будет равна 10/2 = 5, а угол между AB и направлением на центр искомой окружности равен 60 (половине 120 - центр будет лежать на биссектрисе к углу A). То есть имеем прямоугольный треугольник ABO (угол B - прямой) с углом A = 60 градусов и катетом AB = 5. AO = 5/sin(60) = 10.