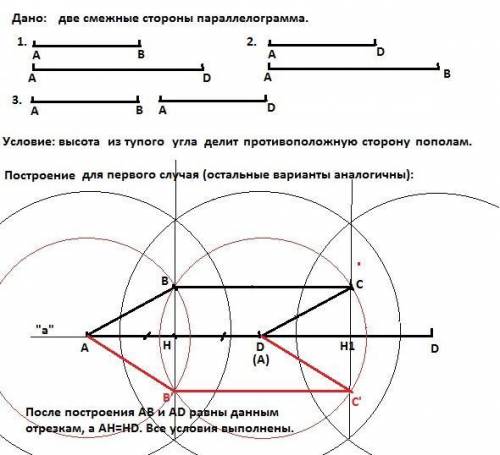
Построения в приложенном рисунке.
Объяснение:
Возможны 2 варианта построения, так как из вершины тупого угла можно провести две высоты к смежным сторонам параллелограмма.
1. На прямой "а" откладываем отрезок, равный одной из данных нам сторон и восстанавливаем к середине этого отрезка перпендикуляр (проведя две окружности радиусом, большим половины отрезка и соединяя точки их пересечения).
2. На прямой "а" откладываем от конца первого отрезка отрезок, равный первому и также восстанавливаем к середине этого отрезка перпендикуляр.
3. Из точек начала и конца первого отрезка, как из центров, проводим окружности радиусом, равным второму данному нам отрезку и в месте пересечения этих окружностей с проведенными перпендикулярами получаем точки - вершины строящегося параллелограмма.
4. Соединяем эти точки и точки начала и конца первого отложенного отрезка и получаем искомый параллелограмм (даже два зеркальных), удовлетворяющий условиям задачи.
P.S. Для второго варианта повторяем построение, начиная строить с отложения на прямой "а" второй данной нам стороны.
Чертим (приблизительно) треугольник ABC со сторонами AC = 4,2, BC = 7 и углом С = 45°.
Опустим высоту BE на сторону АС.
В прямоугольном треугольнике BCE:
∠BEC = 90°
∠BCE = 45°
∠CBE = 180 - 90 - 45 = 45 (°)
Треугольник BCE - прямоугольный равнобедренный с основанием (гипотенузой) BC, боковыми сторонами (катетами) CE = BE
По теореме Пифагора
BC² = CE² + BE²
BC² = 2CE²
(3√2)² = 2CE²
9*2 = 2CE²
CE² = 9
CE = 3 (cм)
BE = 3 (cм)
AC = CE + AE
AE = AC - CE
AE = 7 - 3 = 4 (cм)
В прямоугольном треугольнике ABE:
Катет BE = 3 см
Катет AE = 4 cм
По теореме Пифагора
AB² = BE² + AE²
AB² = 3² + 4² = 9 + 16 = 25
AB = 5 (см)