Поперечний переріз сховища для зберігання овочів має форму рівнобічної трапеції,обчисліть місткість сховища,якщо його довжина 12 ,глибина 1 ,ширина нижньої частини 1 а верхньої 1,4

👇

Ответ:

dbnzgh

20.05.2022

овощехранилище.
ГЕОМЕТРИЯ: призма, сечение которой трапеция.
a=1
b=1,4
h=1
высота призмы Н=12

V=Sперпендикулярного сечения*Н
$V=( \frac{a+b}{2}*h)*H$
$V=( \frac{1+1,4}{2}*1 )*12$

V=14,4 ед. куб

4,8(58 оценок)

Открыть все ответы

Ответ:

Havedid

20.05.2022

В равнобедренной трапеции диагональ является биссектрисой острого угла . Основание трапеции относится к боковой стороне как 8:5 Периметр трапеции равен 69 см найти стороны трапеции.

Объяснение:

АВСД-трапеция, АВ=СД , АД:АВ=8:5 , Р=69 см.

Тк. ВС║АД , АС-секущая , то ∠САД=∠АСД как накрест лежащие .

Тогда ΔАВС-равнобедренный по признаку ⇒АВ=ВС= 5 частей.

Поэтому СД=5 частей. Т.к. АД:АВ=8:5 , то АД= $\frac{8}{5}$ *АВ.

Пусть одна часть равна х см , тогда АВ=ВС=СД=5х , АД= $\frac{8}{5}$ *5х=8х .

Р=АВ+ВС+СД+АД , 69=5х+5х+5х+8х , х= 3 см .

АВ=ВС=СД=15 см , АД= 8см

равнобедренной трапеции диагональ является биссектрисой острого угла основание относится к боковой с

4,8(70 оценок)

Ответ:

Puma20050412

20.05.2022

1) Расположим куб в системе координат так, как показано на рисунке. Точка А - совпадаем с началом координат. Тогда координаты вершин
А(0;0;0) ; В(0;1:0) ; С(1; 1; 0) ; D(1; 0; 0) ; В₁(0;1;1)
Координаты точки М (1; 1/2; 1/2)
Координаты векторов
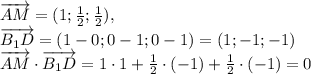
$\overrightarrow{AM}=(1;
 \frac{1}{2}; \frac{1}{2} ), \\ \overrightarrow{B _{1}D 
}=(1-0;0-1;0-1)=(1;-1;-1) \\ \overrightarrow{AM}\cdot \overrightarrow{B 
_{1}D} =1\cdot1+ \frac{1}{2}\cdot(-1)+ \frac{1}{2}\cdot(-1)=0$
Скалярное произведение равно 0, значит векторы ортогональны, прямые AM и B₁D перпендикулярны
Найдем координаты середины отрезка В₁D - точки K
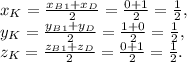
$x
 _{K}= \frac{x_B _{1}+x_D }{2}= \frac{0+1}{2}= \frac{1}{2}, \\ y _{K}=
 \frac{y_B _{1}+y_D }{2}= \frac{1+0}{2}= \frac{1}{2}, \\ z _{K}= 
\frac{z_B _{1}+z_D }{2}= \frac{0+1}{2}= \frac{1}{2}.$
K(1/2; 1/2;1/2)
Найдем координаты середины отрезка АМ - точки Е
$x
 _{E}= \frac{x_A +x_M }{2}= \frac{0+1}{2}= \frac{1}{2}, \\ y _{E}= 
\frac{y_A +y_M }{2}= \frac{1+ \frac{1}{2} }{2}= \frac{1}{4}, \\ z _{E}= 
\frac{z_A+z_M }{2}= \frac{0+ \frac{1}{2} }{2}= \frac{1}{4}.$
E=(1/2; 1/4:1/4)
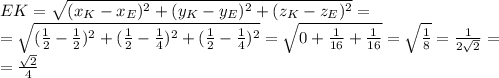
$EK=
 \sqrt{(x_K-x_E) ^{2}+(y_K-y_E) ^{2} +(z_K-z_E) ^{2}} = \\ =\sqrt{( 
\frac{1}{2} - \frac{1}{2} ) ^{2}+( \frac{1}{2} - \frac{1}{4} ) ^{2} +( 
\frac{1}{2} - \frac{1}{4} ) ^{2}}= \sqrt {0+ \frac{1}{16}+\frac{1}{16} 
}= \sqrt{ \frac{1}{8} }= \frac{1}{2 \sqrt{2} }= \\ = \frac{ \sqrt{2} 
}{4}$
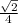
ответ. 1) прямые АМ и В₁D перпендикулярны, угол между ними 90°.2) расстояние между серединами отрезков АМ и В₁D равно $\frac{ 
\sqrt{2} }{4}$

Задача 2. ( см. рис. 2)
В грани ОХZ - квадрат, все стороны которого 1. Диагональ квадрата ОВ имеет длину √2 и легко находится по теореме Пифагора 1²+1²=2²
В прямоугольном треугольнике АВО угол АВО равен 30°, угол АОВ равен 90°, так как ось оу перпендикулярна плоскости ОХZ.
В прямоугольном треугольнике против угла в 30° катет в два раза меньше гипотенузы. Пусть ОА=y, тогда АВ=2y
По теореме Пифагора АВ²=АО²+ВО²
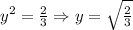
(2y)²=y²+(√2)² ⇒ 3y²=2 ⇒ $y^{2} = \frac{2}{3}\Rightarrow y= \sqrt{ \frac{2}{3} }$
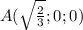
ответ. $A( \sqrt{ \frac{2}{3} };0;0)$

Задача 3.
Так как векторы а и b коллинеарны, то их координаты пропорциональны.
Вектор a имеет координаты (6k; 8k;-7,5k), где k- коэффициента пропорциональности
Так как угол между векторами a и j - тупой, значит их скалярное произведение отрицательно.
Координаты вектора j - (0;1:0)
Найдем скалярное произведение
$
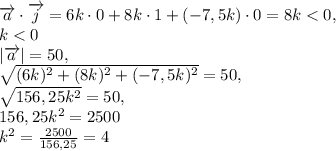
 \overrightarrow{a}\cdot 
\overrightarrow{j}=6k\cdot0+8k\cdot1+(-7,5k)\cdot0=8k$
Так как k<0, то к=-2
ответ. Вектор a имеет координаты (6·(-2); 8·(-2);-7,5·(-2)=(-12; -16; 15)

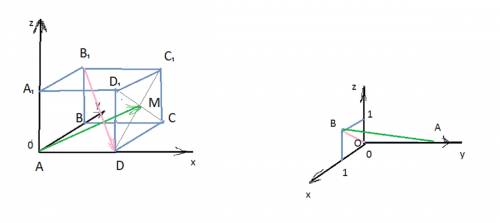
Решить, ! 1. в кубе abcda1b1c1d1 длина ребра равна 1. m - центр грани dd1c1c. используя метод коорди