Точка M равноудалена от сторон ромба и находится на расстоянии 2 см от плоскости ромба. Найдите расстояние от точки M до стороны ромба, если его диагонали равны 16 см и 12 см.
-------
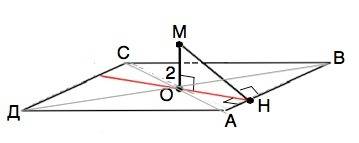
Обозначим ромб АВСД,
Расстояние от точки до прямой равно длине отрезка, проведённого перпендикулярно от точки к данной прямой. =>
отрезок МН перпендикулярен сторонам ромба. МН⊥АВ.
Расстояние от точки до плоскости - длина перпендикуляра между точкой и плоскостью. ⇒ МО перпендикулярен каждой прямой, проходящей через О в плоскости ромба.
т.М равноудалена от сторон ромба, =>
длина проекции ОН отрезка МН равна радиусу вписанной в этот ромб окружности, т.е. ОН равен половине высоты ромба.
а) Диагонали ромба пересекаются под прямы углом и делят его на равные прямоугольные треугольники с катетами, равными их половине.
По т.Пифагора АВ=√(ОН²+ОВ²)=√(36+64)=10 см
б) По ТТП МН⊥АВ => ОН⊥АВ.
ОН можно найти из площади ∆ АОВ
Ѕ(АОВ)=ОА•ОВ:2=24
ОН=24•2:2=4,8
По т.Пифагора МН=√(MO²+OH²)=√(4+23,04)=5,2 см
Через точку М проведем прямую, параллельную B₁D₁ - MN.
Продлим прямую MN до пересечения с ребрами A₁D₁ и A₁B₁. Через получившиеся точки и точку К проведем прямые, которые пересекут ребра DD₁ и ВВ₁ в точках F и Е. KENMF - искомое сечение.
MN - средняя линия ΔB₁C₁D₁. A₁C₁ ∩ MN = T ⇒ A₁T = 3/4 A₁C₁
T∈ (AA₁C₁), K∈ (AA₁C₁), A₁C⊂(AA₁C₁) ⇒ α ∩ A₁C = O
Проведем КК₁ ║ АС в плоскости (АА₁С₁).
ΔАА₁С₁ подобен ΔКА₁К₁ ⇒ А₁К : АА₁ = А₁К₁ : А₁С = КК₁ : АС = 3 : 4, т.е. КК₁ = 3/4 АС,
значит КК₁ = А₁Т.
⇒ ΔА₁ОТ = ΔК₁ОК ⇒ А₁О = ОК₁ ⇒ А₁О = 1/2 А₁К₁
Но А₁К₁ = 3/4 А₁С ⇒ А₁О = 1/2 · 3/4 А₁С = 3/8 А₁С .
Значит, А₁О : ОС = 3 : 5.
Пусть ребро куба равно а.
Тогда А₁К = 3/4а, А₁С₁ = а√2, А₁Т = 3/4·а√2
ΔКА₁Т: tg∠A₁TK = A₁K / A₁T = 3/4a / (3/4·a√2) = 1/ √2
∠A₁TK = arctg (1/√2) - это угол между плоскостью сечения и плоскостью верхнего основания (а значит, и нижнего)