1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
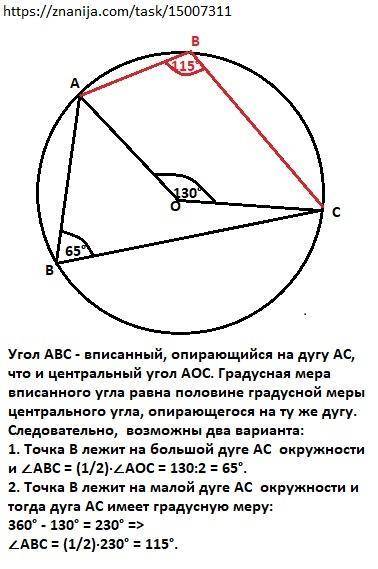
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
Sполн = 2Sосн + Sбок, где Sполн - площадь полной поверхности призмы, Sосн - площадь основания призмы, Sбок - площадь боковой поверхности призмы.
Sбок = P * h, где P - периметр основания призмы, h - высота призмы, равная длине бокового ребра призмы
P = 10 + 12 + 12 = 34 (см)
Sбок = 34 * 8 = 272 (cм²)
В ранобедренном треугольнике ABC:
Боковые стороны AB = BC = 12 (cм)
Основание AC = 10 см
Высота BD, опущенная на основание равнобедренного треугольника, также является медианой и биссектрисой ⇒ делит AC пополам.
AD = 1/2 * AC
AD = 1/2 * 10 = 5 (cм)
В прямоугольном треугольнике ABD:
Гипотенуза AB = 12 см
Катет AD = 5 см
По теореме Пифагора
AB² = AD² + BD²
BD² = AB² - AD²
BD² = 12² - 5²
BD² = 144 - 25
BD² = 119
BD = √119 (cм)
Sосн = 1/2 * AD * BD
Sосн = 1/2 * 5 * √119
Sполн = 2 * (1/2 * 5 * √119) + 272 = 272 + 5√119 ≈ 282,9 (cм²)