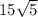 (кв. единица)
(кв. единица)
Объяснение:
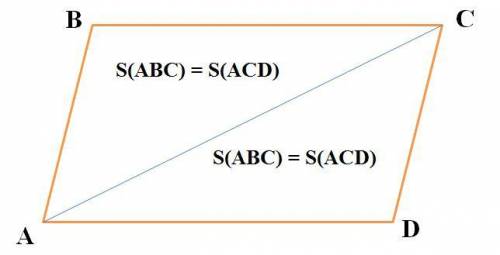
По условию задано координаты трёх его вершин параллелограмма АВСD: А(27;18;20) , В(24;18;16) и С(18;21;18). Так как верно свойство (см. рисунок) "Диагональ параллелограмма делит его на два равных треугольника", то площадь параллелограмма S(ABCD) равна удвоенной площади одного из треугольников, то есть
S(ABCD)=2·S(ABC).
В нашем случае диагональ AC делит параллелограмм на два равных треугольника. Поэтому достаточно найти площадь S(ABC) треугольника ABC по формуле Герона:
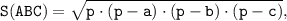
где p - полупериметр: 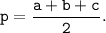
Стороны треугольника ABC находим по формуле расстояния между двумя точками с координатами M(x₁; y₁; z₁) и N(x₂; y₂; z₂):
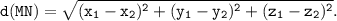
Так как А(27;18;20), В(24;18;16) и С(18;21;18), то
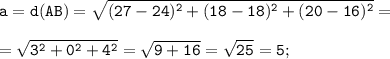
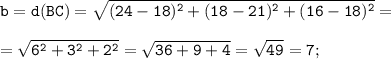
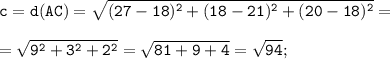
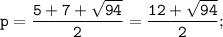
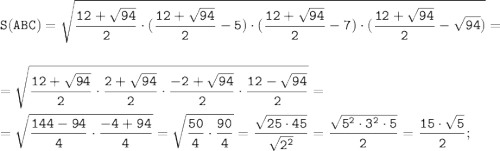
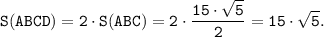
Sбок = P * h, где P - периметр основания призмы, h - высота призмы
P = a + b + c
P = 6 + 10 + 14 = 30 (дм)
h = Sбок / P
h = 300 / 30 = 10 (дм)
Площадь треугольника - основания призмы можно вычислить по формуле Герона:
Sосн =
Полупериметр p = (a + b + c) / 2
p = (6 + 10 + 14) / 2 = 15 (дм)
Sосн =
=
=
Объем прямой треугольной призмы
V = Sосн * h
V = 15√3 * 10 = 150√3 (дм³)