Самая распространенная формула для вычисления площади трапеции - S = (a+b)h/2. Для случая равнобедренной трапеции она явным образом не поменяется. Можно лишь отметить, что у равнобедренной трапеции углы при любом из оснований будут равны (DAB = CDA = x). Так как ее боковые стороны тоже равны (AB = CD = с), то и высоту h можно посчитать по формуле h = с*sin(x).
Тогда S = (a+b)*с*sin(x)/2.
Аналогично, площадь трапеции можно записать через среднюю сторону трапеции: S = mh.
h = диаметру окружности, т. е 6
итак площадь = 6*10=60
Дано :
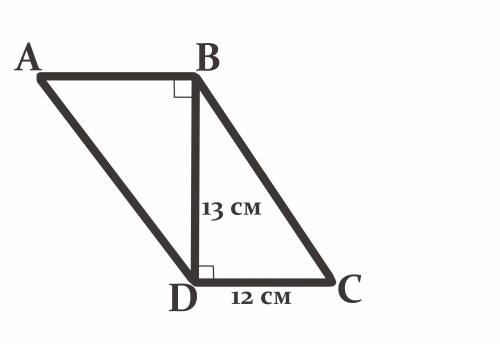
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
гипотенуза по теореме Пифагора AB=c
c^2=a^2+b^2 ; c^2=15^2+20^2=625 ; с=25
высота h от вершины С до гипотенузы c , через площадь треугольника
h*c =a*b ; h = ab/c =15*20/25 = 12
расстояние d от точки D до гипотенузы AB по теореме Пифагора
d^2=H^2+h^2 ; d^2=35^2+12^2=1369 d=37 м
ОТВЕТ 37 м