Меньший из отрезков на которые центр описанной около равнобедренного треугольника окружности делит его высоту, равен 8 см, а основание треугольника равно 12см. найти площадь этого треугольника
Обозначим четырёхугольник АВСД, центр окружности О. У вписанного четырёхугольника сумма противоположных углов равна 180 градусов. Значит, противоположные углы - это А; С (120°; 60°) и В; Д ( 150°; 30°). Проведём радиусы в вершины. Так как по условию ВС = АВ, то ОВ делит угол в 150° на 2 по 75°. Треугольники ОСВ и ОВА равнобедренные, угол ВАО тоже 75°. Тогда угол ОАД равен 120°-75 = 45°. Угол АОД равен 180°-45°-30° = 105°. Дуга АВС, на которую опирается вписанный угол Д, равна 30*2 = 60°. Так как она делится пополам, то получаем ответ: Дуги равны: АВ = ВС = 30°, АД = 105°, ДОС = 360°-2*30°-105° = 195°.
BO = AO ⟹ OD – меньшая часть высоты BD, т.к. катет меньше гипотенузы.
По т. Пифагора:
BO =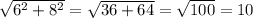
BD = 10 + 8 = 18
SΔ = 1/2AC * BD = 1/2 * 12 * 18 = 108 см²