Объяснение:
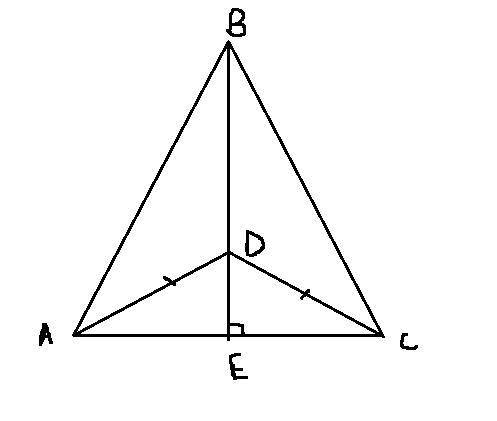
Пусть BE - высота, проведенная к стороне AC, а точка D - равноудалена от концов AC, значит AD=DC. Рассмотрим тр-ки ADE и CDE. Они прямоугольные и у них один из катетов общий (DE), а гипотенузы равны AD=DC. Значит эти тр-ки равны: "если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны."
Из их равенства следует, что AE=EC, а значит тр-к ABC равнобедренный по признаку: "Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным"
Дано:
Р = 30 см
а - основание равнобедренного треугольника
b - боковая сторона равнобедренного треугольника
1) а - b = 3 cм
2) b - a = 3 cм
Найти:
а и b
Периметр равнобедренного треугольника равен
Р = а + 2b
1) Из выражения а - b = 3 cм найдём а = b + 3
Тогда периметр
Р = b + 3 + 2b
P = 3b + 3
По условию
Р = 30cм
30 = 3b + 3
3b = 27
b = 9
a = 9 + 3 = 12
Проверим неравенство треугольника
Длина любой стороны треугольника всегда меньше суммы длин двух его других сторон
9 < 9 + 12
12 < 9 + 9
Неравенство треугольника выполняется, значит, стороны треугольника равны: 9 см; 9 см и 12 см
2) Из выражения b - а = 3 cм найдём а = b - 3
Тогда периметр
Р = b - 3 + 2b
P = 3b - 3
По условию
Р = 30cм
30 = 3b - 3
3b = 33
b = 11
a = 11 - 3 = 8
Проверим неравенство треугольника
Длина любой стороны треугольника всегда меньше суммы длин двух его других сторон
8 < 8 + 11
11 < 8 + 8
Неравенство треугольника выполняется, значит, стороны треугольника равны: 11 см; 11 см и 8 см
1) 9 см; 9 см и 12 см
2) 11 см; 11 см и 8 см
Sосн=√3*a²/4
a=a/9
H=H*3
Vн=3H*(Sосн/81)/3=HSосн/81
Vн/V=1/27
Объём пирамиды уменьшится в 27 раз
12/27=4/9 дм³
Объём получившейся пирамиды 4/9 дм³