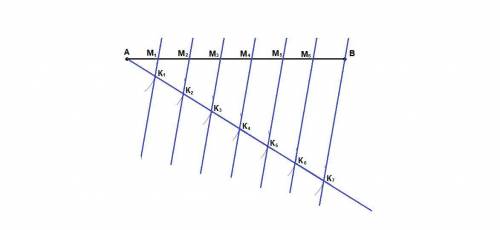
АВ - произвольный отрезок.
1. Проведем луч с началом в точке А под произвольным углом к отрезку.
2. На луче от точки А с циркуля отложим 7 одинаковых отрезков произвольной длины:
АК₁ = К₁К₂ = К₂К₃ = К₃К₄ = К₄К₅ = К₅К₆ = К₆К₇
3. Проведем прямую К₇В через конец последнего отрезка и точку В.
4. Через точки К₁, К₂, К₃, К₄, К₅ и К₆ проведем прямые, параллельные прямой К₇В.
Точки пересечения этих прямых с отрезком АВ разделят отрезок АВ на 7 равных частей (по теореме Фалеса)
АМ₁ = М₁М₂ = М₂М₃ = М₃М₄ = М₄М₅ = М₅М₆ = М₆В
Преобразуем в левой части по формуле дополнительного угла.
Здесь лучше воспользоваться от суммы синусов к произведению
sin(2x+π/12) = 0
2x + π/2 = πk,k ∈ Z
x = -π/4 + πk/2, k ∈ Z
cos(x+π/12) = 0
x + π/12 = π/2 + πn,n ∈ Z
x = 5π/12 + πn,n ∈ Z