1. Поскольку CO – биссектриса угла ACB, а треугольник ABC – равнобедренный, то CO ⊥ AB. Углы ABO и BCO равны, так как каждый из них в сумме с углом BOC составляет 90°. Следовательно, ∠ACB = 2∠BCO = 2·40° = 80°.
ответ: 80°.
2. Перпендикуляр, проведенный из центра окружности к хорде, делит её пополам. ⇒
АС=ВС=20:2=10
ОА=ОВ - радиусы. ⇒∆ АОВ- равнобедренный.
Углы при основании равнобедренного треугольника равны.
∠ОВА=∠ОАВ=45°⇒ ∠АОВ=90°
ОС⊥АВ. ОС- высота, медиана и биссектриса прямоугольного ∆ АОВ и делит его на два равных равнобедренных.
СО=АС=СВ=10 см
ответ. 10 см.
3. Вот так. Только во второй задаче бери радиус больше половины отрезка
В прямокутному трикутнику катет довжиною 15 см прилягає к куту 30°. Знайдіть бісектрису другого гострого кута цього трикутника.
В прямоугольном треугольнике катет длиной 15 см прилегает к углу 30 °. Найдите биссектрису второго острого угла этого треугольника.
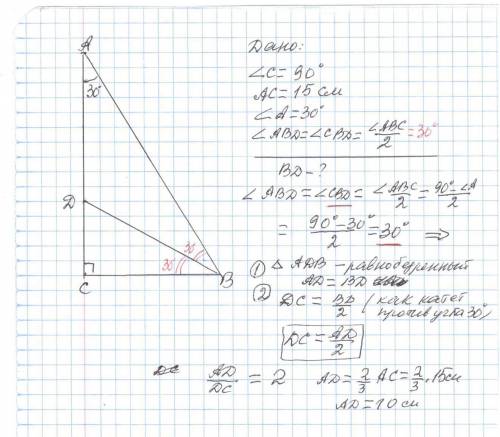
Дано :
∠C =90° ;
AC =15 см ;
∠A =30 ° ;
∠ABD =∠CBD = ∠ABC /2 ( BD _биссектриса )
-----------------
BD - ?
∠ABC = 90° - ∠ A =90° -30° =60°
∠ABD =∠CBD = ∠ABC /2 = 60°/2 = 30° , следовательно
1. ΔADB равнобедренный AD = BD и
2. из ΔDBC: CD = BD /2 как катет против угла ∠CBD =30°
CD / AD = 1/2 ⇔ 1 +CD / AD = 1/2 +1 ⇔AC/AD =3/2 ⇒AD =(2/3)*AC
AD =2*15 см / 3 = 10 см
ответ : BD= AD = 10 см .
- - - - - - - - - -
2-ой
CD /AD = BC / BA ( теорема о биссектрисе )
CD /AD =1/2 BC = BA/2 (снова как катет против угла A =30°)
* * * * * * * рисунок во приложении * * * * * * *
P abc=143 см, то P=AC+BC+AB, AC=P-BC-AB=143-42-35=66 см
ответ. AC=66 см