
1) Прямоугольный параллелепипед описан около цилиндра. радиус основания которого равен 4. а высота 5. Найти объем параллелепипеда
Все грани прямоугольного параллелепипеда -прямоугольники. Основания вписанного цилиндра - окружности, вписанные в основания параллелепипеда, а его высота является и высотой параллелепипеда.
Если в прямоугольник вписана окружность - этот прямоугольник - квадрат.
Стороны основания параллелепипеда равны диаметру оснований цилиндра.
а=2r=8
Объем прямоугольного параллелепипеда равен произведению его трех измерений.
V=S*H=8*8*5=320 (единиц объема)
----------------------
2) Радиус основания конуса равен 15, расстояние от центра до образующей равно 12. Найти площадь боковой поверхности конуса.
формула площади боковой поверхности конуса
S=πRL
Расстояние от центра основания до образующей - в данном случае высота прямоугольного треугольника ВОС, образованного высотой ВО конуса, радиусом ОС и образующей ВС (она же гипотенуза треугольника ОВС)
∆ ОНС - египетский ( отношение катета и гипотенузц 3:5). Значит, НС=9 ( можно найти по т.Пифагора)
ОС - катет ∆ ОВС.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.
. ОС²=ВС*НС
225=ВС*9
ВС=225:9=25
S=π*15*25=375 (ед. площади)
-----------------------------
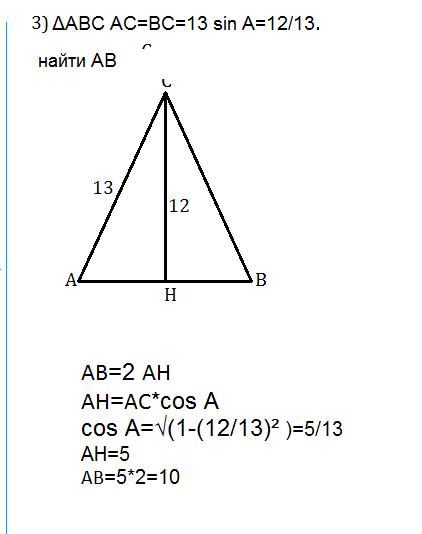
В ΔABC: AC=BC=13, sin ∠A=12/13. Hайти АВ
СН- высота ∆ АВС
АВ=2 АН
АН=АС*cos A
cos A=√(1-(12/13)² )=5/13
AH=5
АВ=5*2=10

Отношение сторон треугольника АВD- 12:16:20=3:4:5. Это отношение сторон "египетского" треугольника, значит, ∆ АВD- прямоугольный. (Можно проверить по т.Пифагора)
∆ ВСЕ - прямоугольный по построению, т.к. СЕ⊥BD.
ВС||AD, ⇒ ∠СВD=∠BDA как накрестлежащие. Если острый угол одного прямоугольного треугольника равен острому углу другого, они подобны.
∆ BEC ~ ∆ ABD.
Тогда ∠ВСЕ=∠ВАD, и их тригонометрические функции равны.
sin ВСЕ=sin A=BD/AD=16/20=0,8
cos ВСЕ=cos A=AB/AD=12/20=0,6
tg BCE=tg A=BD/AB=16/12=4/3
