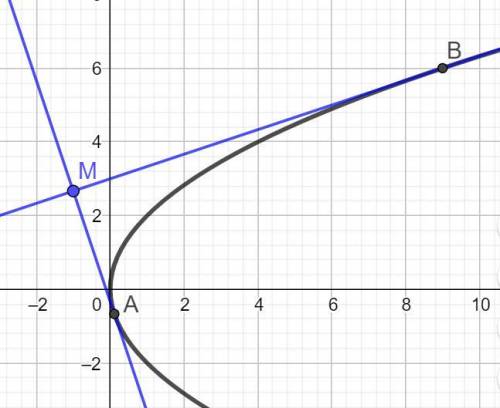
Уравнение параболы y^2=4x выразим через у: y = ±2√x, что соответствует двум ветвям параболы выше и ниже оси Ох.
Пусть абсцисса точки касания хо.
Общее уравнение касательной: y = y(xo) + (y'(xo))(x - xo).
Производные равны: y' = ±(1/xo).
Подставляем данные для верхней ветки, получаем:
y = 2√xo + (1/√xo)*(x - xo) = (2xo + x - xo)/√xo = (xo + x)/√xo.
Так как прямая проходит через точку М(-1, (8/3)), то:
(8/3) = (xo - 1)/√xo.
Возведём обе части уравнения в квадрат.
(64/9) = (xo² - 2xo + 1)/xo.
9xo² - 18xo + 9 = 64xo. Получаем квадратное уравнение:
9xo² - 82xo + 9 = 0.
D=(-82)^2-4*9*9=6724-4*9*9=6724-36*9=6724-324=6400;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(2root6400-(-82))/(2*9)=(80-(-82))/(2*9)=(80+82)/(2*9)=162/(2*9)=162/18=9;
x_2=(-2root6400-(-82))/(2*9)=(-80-(-82))/(2*9)=(-80+82)/(2*9)=2/(2*9)=2/18=1/9~~0.111111111111111.
Имеем 2 абсциссы точек касания, значит, касательных будет две.
Вторая точка соответствует нижней ветви параболы, так как уравнение касательной одинаковое.
Координаты точек касания B(9; 6), A((1/9); (-2/3)).
Уравнения касательных имеют вид:
y(B) = (1/3)x + 3,
y(A) = -3x - (1/3).
Цилиндр описан около сферы.
R цилиндра = 2 см.
Найти:S полн поверхности цилиндра - S полностью поверхности сферы = ?
Решение:Так как в данный цилиндр вписана сфера, по условию ⇒ D сферы = h цилиндра.
R цилиндра = R сферы = 2 см (так как в цилиндр вписана сфера).
⇒ D сферы = h цилиндра = R сферы * 2 = 2 * 2 = 4 см.
S полн поверхности цилиндра = 2πR(R + h), где R - радиус цилиндра; h - высота цилиндра.
S полн поверхности цилиндра = π(2 * 2(2 + 4) = 24π см²
S полной поверхности сферы = 2πR² , где R - радиус сферы.
S полной поверхности сферы = π(4 * 2²) = 16π см²
⇒S полн поверхности цилиндра - S полн поверхности сферы = 24 - 16 = 8π см²
ответ: 8π см²